調波打楽器音分離: 列車走行音からの継ぎ目音分離

第1R&Dの豊田です。この記事では音源分離技術の一つである、調波打楽器音分離を用いて列車走行音から動力音と継ぎ目音を分離します。継ぎ目音とは、列車の車輪が線路と線路のつなぎ目を通過する時に鳴る「ガタンゴトン」という音です。

列車走行音からの継ぎ目音分離

この記事の目的は列車走行音から動力音と継ぎ目音を分離して取り出すことです。まず最初に、走行音を以下に示します。

動力音がだんだんと静かになる中、継ぎ目音が何回か聞こえるので確認してみて下さい。次にこの音のスペクトログラムを以下に示します。源信号の短時間フーリエ変換を\(X(t,f)\)と置くとスペクトログラムは

$$S(t,f)=|X(t,f)|$$

と書くことが出来ます。ここで\(t\)と\(f\)は時間と振動数を表します。

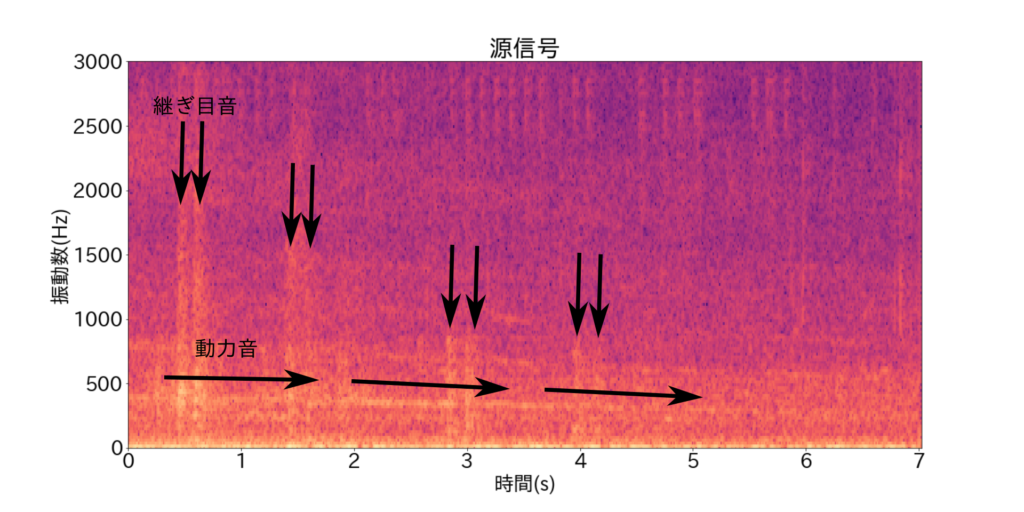
スペクトログラムを見てみると、図中の矢印で示した、二種類の目立つ構造が存在していることが分かります。

• 動力音: 時間方向に広く分布し、ある周波数帯に局在している、「横方向の音」（調波音）
• 継ぎ目音: ある時間帯に局在し、周波数方向に広く分布している、「縦方向の音」（打楽器音）

動力音、継ぎ目音はそれぞれ調波音(harmonic)、打楽器音(percussion)の性質をもっています。ピアノ音など音楽中で音色を構成する音を調波音といいます。また、ドラム音など音楽中で突発音を構成する音を打楽器音といいます。調波打楽器音分離(Harmonic Percussion Source Separation, HPSS)を用いると調波音、打楽器音を源信号から上手く分離することができます。以下では計算を行う前に調波打楽器音の手法について簡単に述べます。

調波打楽器音分離(HPSS)

ここではD. FitzGerald（参考文献 [1]）による手法を用います。スペクトログラムのある振動数帯に存在する調波音を取り出すために、その振動数帯に注目して時間方向にメディアンフィルターを適用します（下図参照）。調波音は時間方向に長い帯を形成しているため、時間方向にメディアンを演算しても生き残りますが、打楽器音はある時間帯に局在しているため、メディアンが演算されることによって消えます。時間方向にメディアンフィルターをスペクトログラムに適用した結果を\(S_\parallel(t,f)\)と書いておきます。

また、スペクトログラムのある時間帯に存在する打楽器音を取り出すためには、その時間帯に注目して周波数方向にメディアンフィルターを適用します（下図参照）。打楽器音は周波数方向に広く分布しているため、周波数方向にメディアンを演算しても生き残りますが、調波音はある周波数帯に局在しているため、メディアンが演算されることによって消えます。周波数方向にメディアンフィルターを適用した結果を\(S_\perp(t,f)\)と書いておきます。

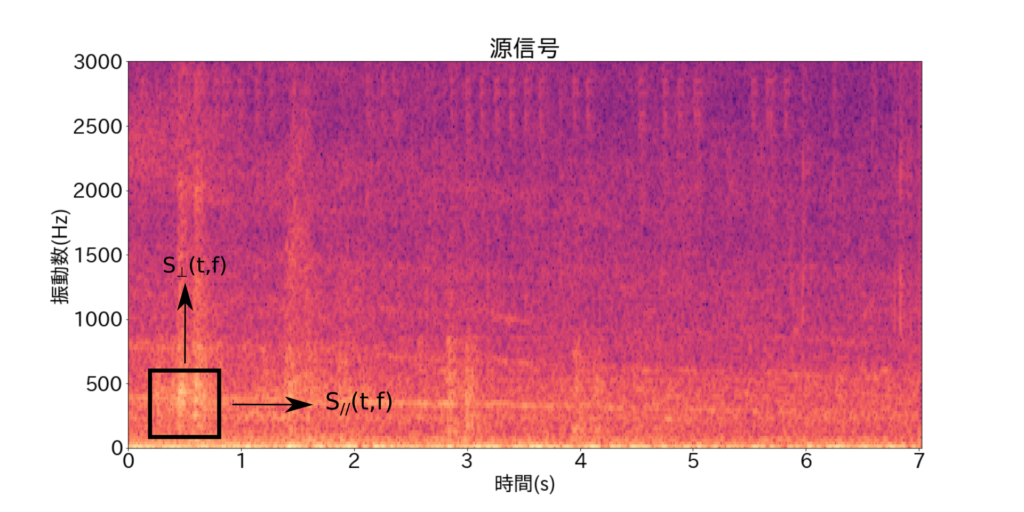
スペクトログラムにメディアンフィルターを適用した結果\(S_\parallel(t,f)\)、\(S_\perp(t,f)\)を用いて動力音（調波音）、継ぎ目音（打楽器音）を取り出すためのウィーナーフィルター\(M_{\rm H}(t,f)\)、\(M_{\rm P}(t,f)\)を以下のように構成します。

$$\begin{eqnarray}
M_{\rm H}(t,f)=\frac{S_{\parallel}(t,f)}{S_{\parallel}(t,f)+S_{\perp}(t,f)}, \\
M_{\rm P}(t,f)=\frac{S_{\perp}(t,f)}{S_{\parallel}(t,f)+S_{\perp}(t,f)}
\end{eqnarray}$$

これらを用いると、動力音（調波音）、継ぎ目音（打楽器音）の短時間フーリエ変換\(X_{\rm H}(t,f)\)、\(X_{\rm P}(t,f)\)は以下で求められます。

$$\begin{eqnarray}
X_{\rm H}(t,f)&=&M_{\rm H}(t,f)\odot X(t,f), \\
X_{\rm P}(t,f)&=&M_{\rm P}(t,f)\odot X(t,f)
\end{eqnarray}$$

\(X(t,f)\)は源信号の短時間フーリエ変換です。また、記号\(\odot\)は行列の要素毎の積（アダマール積）を表しています。

源信号から分離された動力音（調波音）、継ぎ目音（打楽器音）をそれぞれ\(x_{\rm H}(t)\)、\(x_{\rm P}(t)\)と置くと、これらは上の結果を用いて、

$$\begin{eqnarray}
x_{H}(t)&=&\mathcal{F}^{-1}\left[X_{\rm H}(t,f)\right], \\
x_{P}(t)&=&\mathcal{F}^{-1}\left[X_{\rm P}(t,f)\right]
\end{eqnarray}$$

と計算されます。ここで記号\(\mathcal{F}^{-1}\)は逆フーリエ変換を表します。

計算

librosaに実装されている調波打楽器音分離、librosa.decompose.hpssを用いて実際に計算を行います。まず最初にスペクトログラムを関数に渡し、動力音（調波音）、継ぎ目音（打楽器音）を抽出するためのウィーナーフィルターを計算します。続いて、得られたフィルターを源信号の短時間フーリエ変換に乗じて、動力音（調波音）、継ぎ目音（打楽器音）の短時間フーリエ変換を抽出します。

import librosa

# 源信号の短時間フーリエ変換の絶対値abs(stft)を入力し、
# 調波音、打楽器音を分離するためのウィーナーフィルターH_mask, P_maskを計算する。
H_mask, P_mask = librosa.decompose.hpss(abs(stft), kernel_size=(51,51), mask=True)

# 上で計算したウィーナーフィルターを源信号の短時間フーリエ変換に乗じて
# 調波音、打楽器音のスペクトログラムH、Pを計算する。
H = H_mask*stft
P = P_mask*stft

5行目で、kernel_sizeは時間方向、振動数方向のメディアンフィルターのサイズです。また、ウィーナーフィルターを返り値として受け取るためにはフラグmaskをTrueにする必要があります。下図に抽出された動力音、継ぎ目音のスペクトログラム\(|X_{\rm H}(t,f)|\)および\(|X_{\rm P}(t,f)|\)を示します。

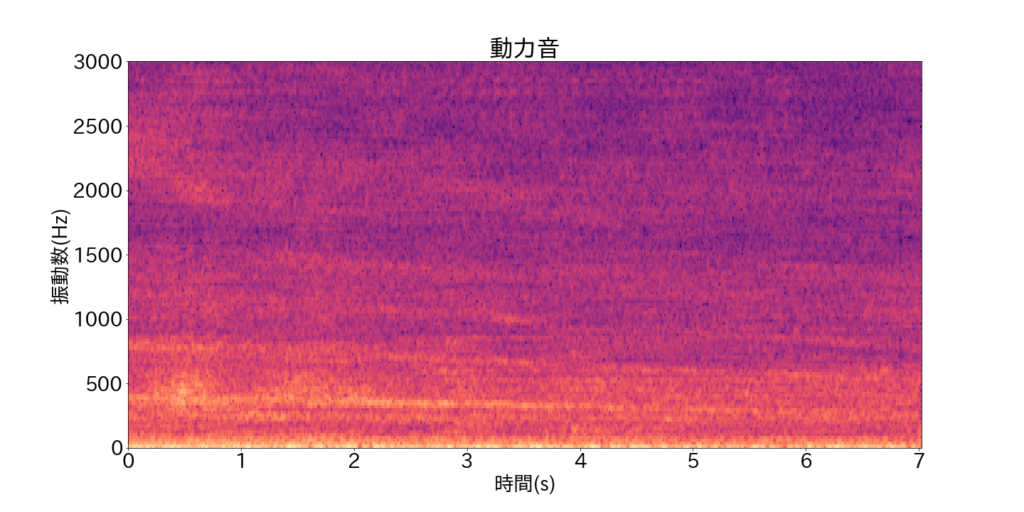
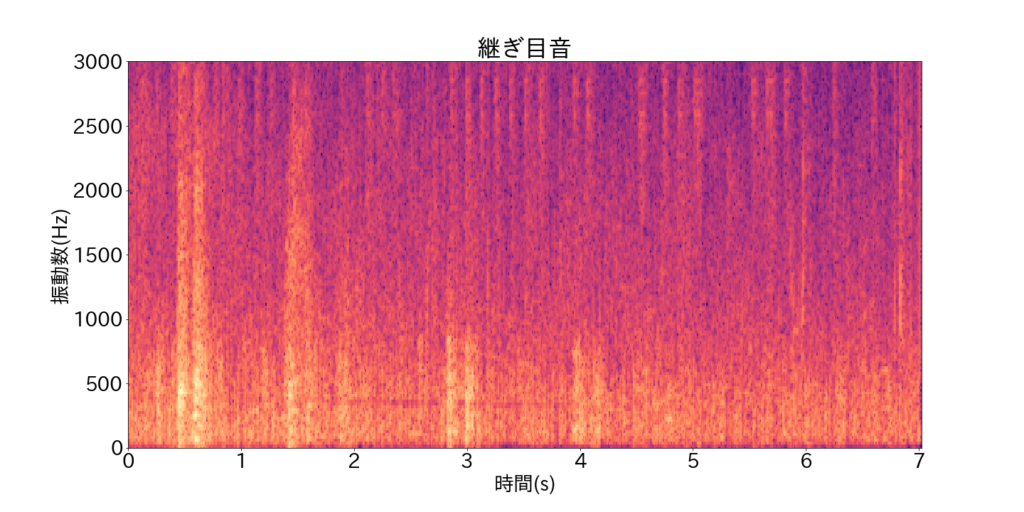
動力音からは継ぎ目を表す「縦線」が、継ぎ目音からは動力音を表す「横線」が消えていることが分かります。最後に、動力音、継ぎ目音のスペクトログラムを逆短時間フーリエ変換して、音にします。

# hop_length、win_lengthは短時間フーリエ変換に用いたホップ長、ウィンドウ幅
H_wav = librosa.istft(H, hop_length=hop_length, win_length=win_length)
P_wav = librosa.istft(P, hop_length=hop_length, win_length=win_length)

得られた音を示します。

完璧ではないものの、上手く分離できました。

まとめ

この記事では調波打楽器音分離を紹介しました。この手法を用いることによって、源信号のスペクトログラムから調波音部分（ピアノなどが奏でる音楽の音色部分）と打楽器音部分（ドラムなどが発する突発音）を分離することができます。さらにこの記事では、この手法を用いて列車走行音のスペクトログラムから動力音部分と継ぎ目音部分を分離しました。動力音、継ぎ目音がそれぞれ調波音、打楽器音の性質を持つことを利用して、調波打楽器音分離により両者をスペクトログラムから上手く分離することができました。

参考文献

[1] Fitzgerald, Derry. “Harmonic/percussive separation using median filtering.” 13th International Conference on Digital Audio Effects (DAFX10), Graz, Austria, 2010.