こんにちは。第1R&Dセンターの魏です。
私は一番好きな数字は0です。なぜかというと、正数でもないし負数でもない特別な存在だからです。1世紀頃、無名なインド人が、はじめて「0」を使ったといわれています。この0は、インド人の言葉で「空(から)」の意味を表します。我々の勉強、仕事、生活も初めは全てゼロからです。
今回は「ゼロからわかる」と題して、技術の解説を行います。
(HMくんが乱入してきました。)
え?ゼロからわかるだって?変な名前だね。
あ。HMくんじゃないか。
こんにちは、今日はどうしたの?
こんにちは、魏さん。
ここでは色々な技術についての質問に答えてもらえると聞いたんだけど・・・。
僕も最近疑問に思ってることがあって・・・。
どんな質問?
最近周りで音声を勉強している人達が「STFT、STFT」言っているんだけど、あれは何なの?
それでは、ヒントをあげましょう。
STFTは英語のShort-Time Fourier Transformの略語です。
日本語では何というでしょう?
うーん、短い時間・・・フーリエ変換・・・?
短時間フーリエ変換かな?
名前はなんとなく聞いたことがあるけど、意味が全然わからない・・・。
よく分かりましたね。
そうです、短時間フーリエ変換です。
短時間フーリエ変換を理解するためには、その前にフーリエ変換を理解する必要があります。
じゃあ、まずはフーリエ変換を教えて。
そのフーリエ変換を教える前に、必要な数学の知識を確認してもいいかな?
え・・・数学苦手なんだけど・・・。
大丈夫、ゆっくり考えてもいいですよ。
最初は指数関数について、指数関数は「足し算とかけ算の橋」です。
特に複素指数関数は回転を表示することができます。
\(e^{\pi i}\)は単位円で左に180度で回転します。
\(e^{\pi i}\)・・・単位円・・・。
どっかに見たことある気がする・・・。
正解はTHE世界公式ランキングの第二位のオイラーの公式\(e^{i \pi}+1=0\)です。
ちなみに、フーリエ変換は第七位でした。
へーそうなんだ。
さっき言ってた、「たし算とかけ算の橋」ってどういう意味?
数値軸上において、たし算は平行移動、かけ算は伸縮を意味します。
例えば座標点\((1,0)\)を\((0,1)\)にたし算の方法で移動する場合、まず横軸方向に\(-1\)平行移動、次に縦軸方向に\(+1\)平行移動することで目標の座標点へ到達します。
それは分かるんだけど・・・。
例えば点\((1,0)\)から点\((-1,0)\)への移動であれば、平行移動の他に回転でも移動出来そうじゃない?
いい考えですね。
複素数には\(-1=i×i\)という面白い決まりがあります。
点\((1,0)\)から点\((-1,0)\)へ移動する場合、\(i\)を2回かける操作をすればいいことになります。
これが何を意味するか分かりますか?
2回かけ算を行う事で180度回転するなら、\(i\)は90度回転だよ。
そういえば、点\((1,0)\)から左回転90度すると、ちょうど縦軸の\((0,1)\)になってるね。
同じ長さだ。なんか不思議な
そうです。
縦軸が複素数\(i\)が付いた虚数軸であれば、回転ができますね。
今までたし算(平行移動)で表現してきた座標系を、かけ算に変換ができるようになります。
でも、\(i\)は回転?ちょっと理解できないな。
回転というのは円の周りを移動することを意味していますよね。
それで?
先程言った通り、指数関数は橋です。
今回は指数関数\(f(x)=a^x\)を使います。
\(a=e\)と置いた時のマクローリン展開は分かりますか?
うん、これは簡単や。
\begin{align}
e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \quad(-\infty < x < \infty)
\end{align}
よくできました。
この式に\(x=i \theta\)入れると、以下のようになります。
\begin{align}
e^{i \theta} &= 1 + {i \theta} + \frac{1}{2!}({i \theta})^2 + \frac{1}{3!}({i \theta})^3 + \frac{1}{4!}({i \theta})^4 + \frac{1}{5!}({i \theta})^5 + \cdots\\
&= (1 – \frac{{\theta}^2}{2!} + \frac{{\theta}^4}{4!} + \cdots) + i(\theta – \frac{{\theta}^3}{3!} + \frac{{\theta}^5}{5!} + \cdots)
\end{align}
\(\sin (x)\)、\(\cos (x)\)のマクローリン展開はそれぞれ、
\begin{align}
\sin (x) = x – \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots\\
\cos (x) = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} + \cdots
\end{align}
となることから、上の式は以下のように表すことができます。
\begin{align}
e^{i \theta} = \cos{\theta} + i \sin{\theta}
\end{align}
この式には何の意味があるの?
この式は可視化すると以下のようになります。
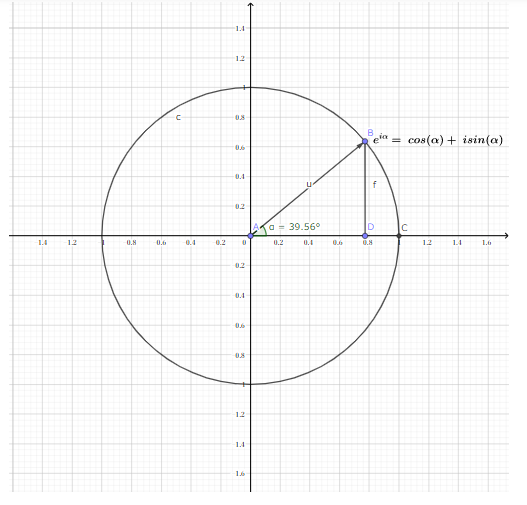
仮に縦軸は複数\(i\)を含める、\(\sin (\theta)\)は縦軸、\(\cos (\theta)\)は横軸、そうなら、\(e^{i \theta}\)は円心は原点、半径は1の円でした。\(e^{i \theta}\)は回転になりました。\(\theta\)は回転の度数、\(\theta = 2 \pi\)の時360度を回転して、円になります。
これ。。。。もしかして、伝説の複素表面なの?
そのとおり!次の図を見てください。
左側の図を指数関数\(f(x) = 2^x\)を用いて右側の図に変換しています。
左側の座標での横軸移動は、右側の座標では伸縮になります。
左側の座標での縦軸移動は、右側の座標で回転になります。
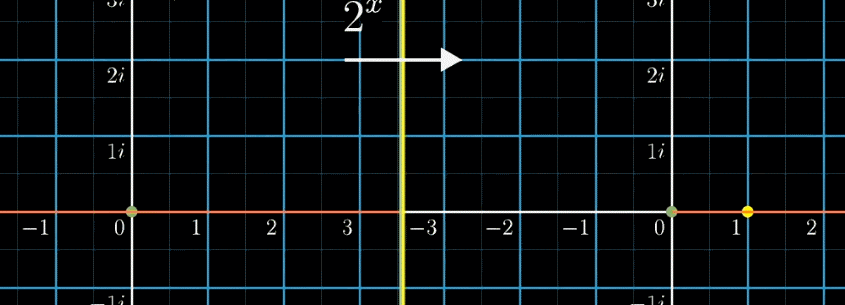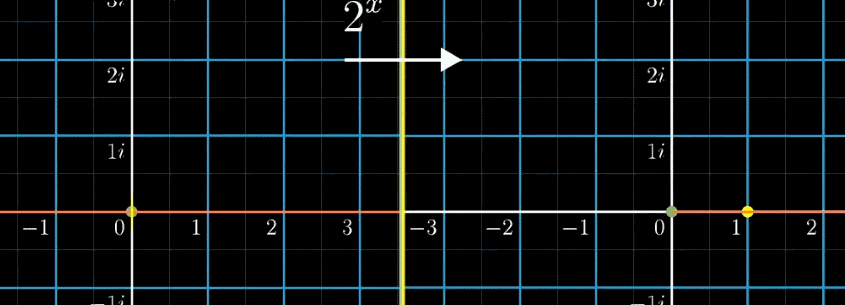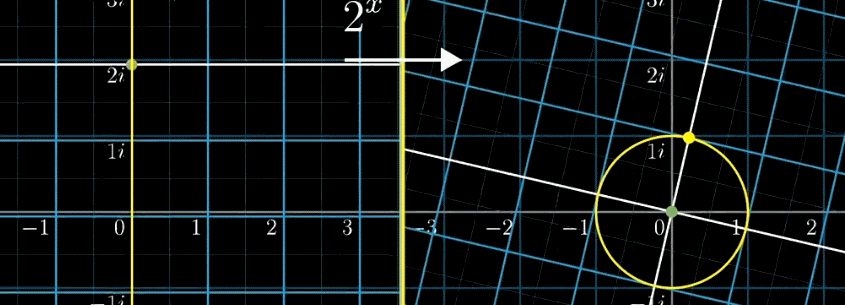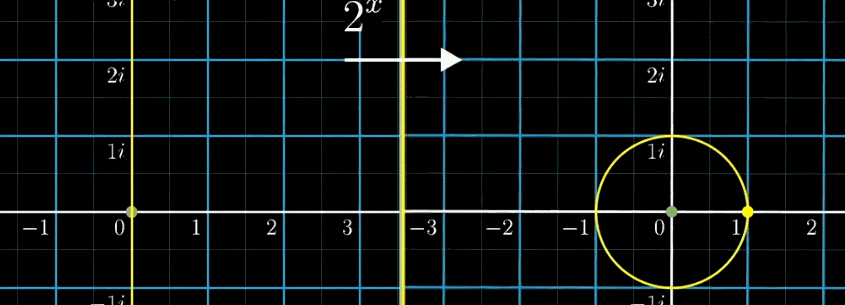
これは凄い・・・。
ここでは\(f(x) = 2^x\)を使ってるけど、さっき出た\(e^{i \theta}\)は半径が1の円だから、\(f(x) = e^x\) を使ったらもっと分かりやすいと思うんだけど・・・。
いいアイデアですね。それならもっと円の意味が分かりそうですね。
下の図は指数関数\(f(x) = e^x\)で変換した例です。
\(e^{i \pi}\)で左半周回り、ちょうど\((-1,0)\)になりました。
オイラーの公式\(e^{i \pi}+1=0\)を可視化するとこのようになります。
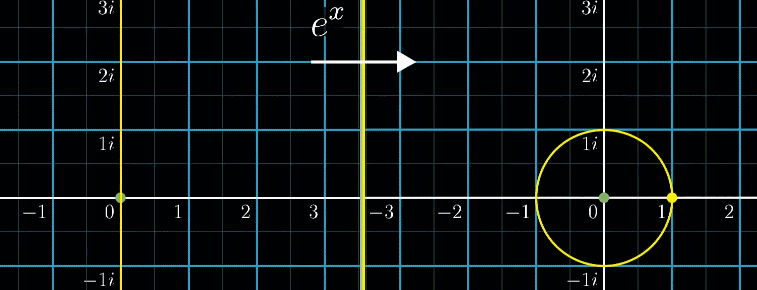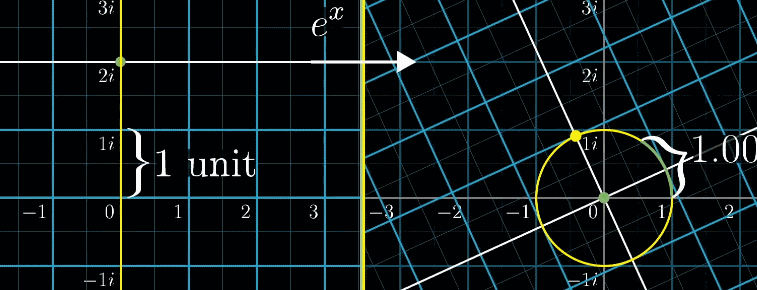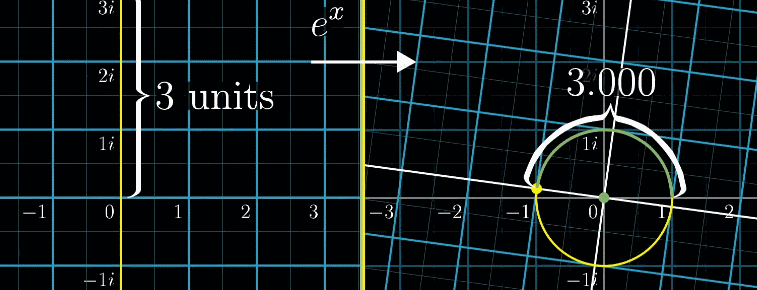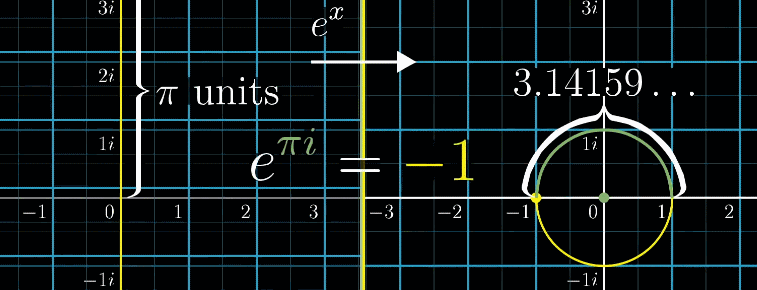
これオイラーの公式か。なんか不思議。
\(e^x\)において、\(x = ai\)は複素平面上の回転、\(a\)は円の周りの長さを表してるんだね。
でも、これとフーリエ変換は何の関係あるの?
\(e^{i \pi}\)はフーリエ変換において非常に重要な要素です。
フーリエ変換の公式は\(\hat{f}(\xi) = \int^{\infty}_{-\infty} f(x) e^{-2 \pi i x \xi} dx\)と表します。
このとき、\(\xi\)は任意の実数です。
ほんとだ!\(e^{i \pi}\)が出てきた!
でも式が複雑すぎるなぁ・・・。
この式はあとで説明します。
音はどうのような物理現象で成り立っているか分かりますか?
気圧の振動かな?
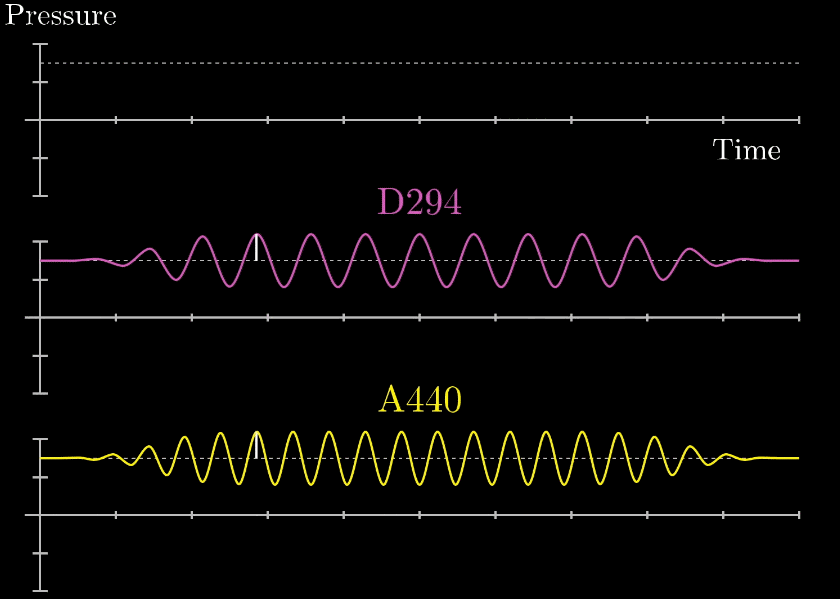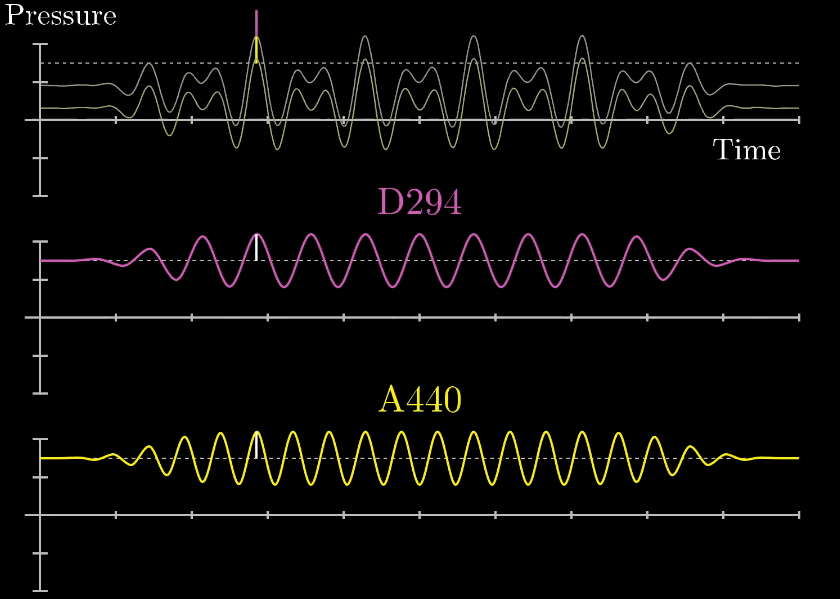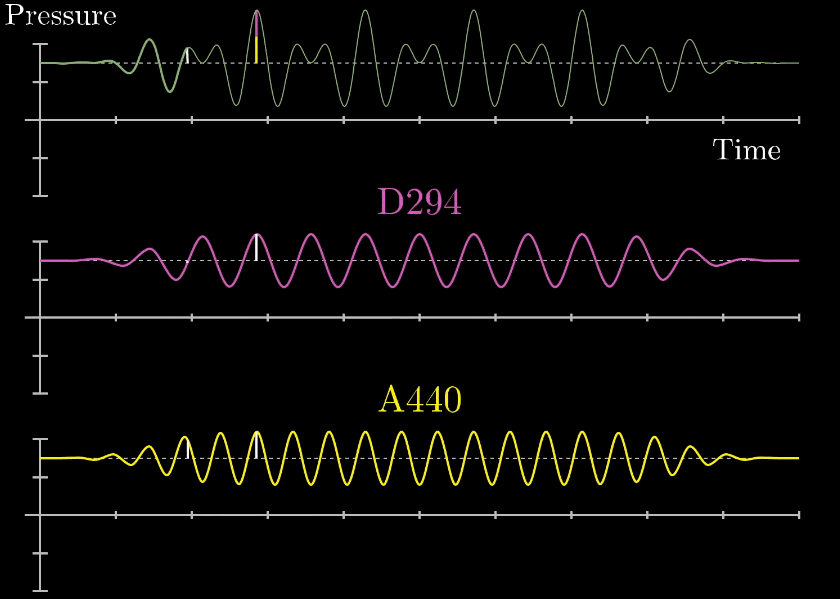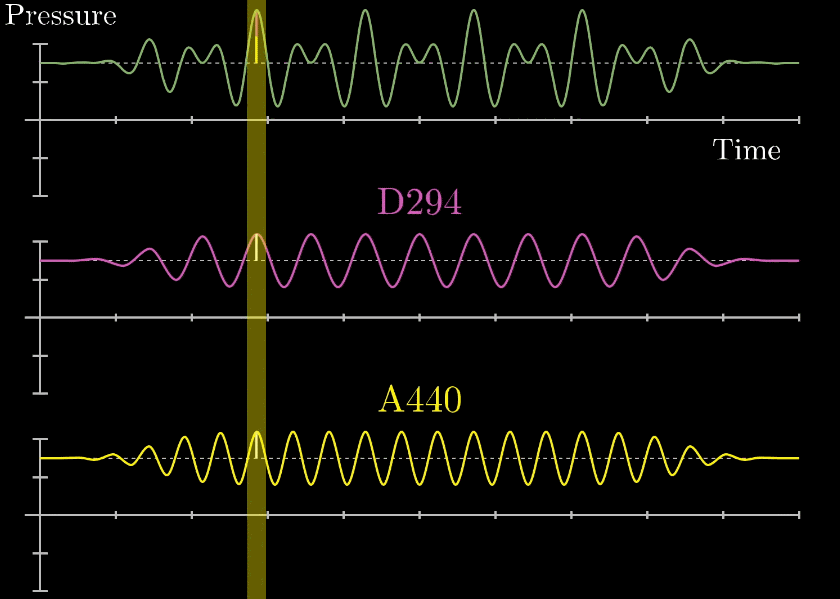
その通りです。下の図を見てください。
黄色いの線は周波数440Hz(一秒で440回振動)の音声です。
紫の線は周波数294Hz(一秒で294回振動)の音声です。
この二つ音は単純な正弦波(\(\sin\)波)ですが、二つの音が合わさることにより上の緑線になります。
緑線は黄色線と紫線の振幅を時間ごとにたし算したものです。
フーリエ変換はどんな複雑な波形も同じ形を繰り返す周期性を持った波であれば、複数の単純な正弦波で表現できます。
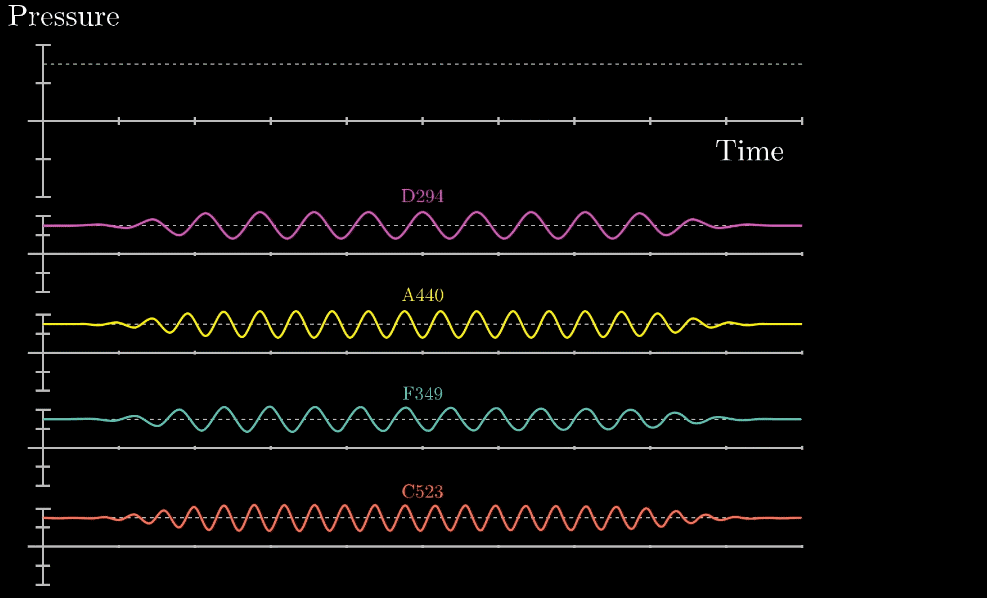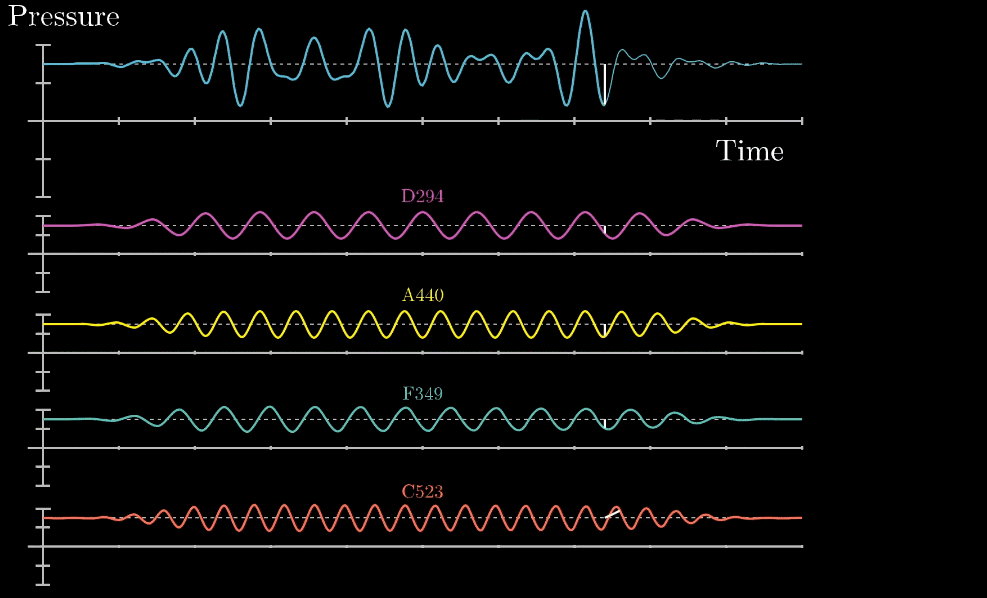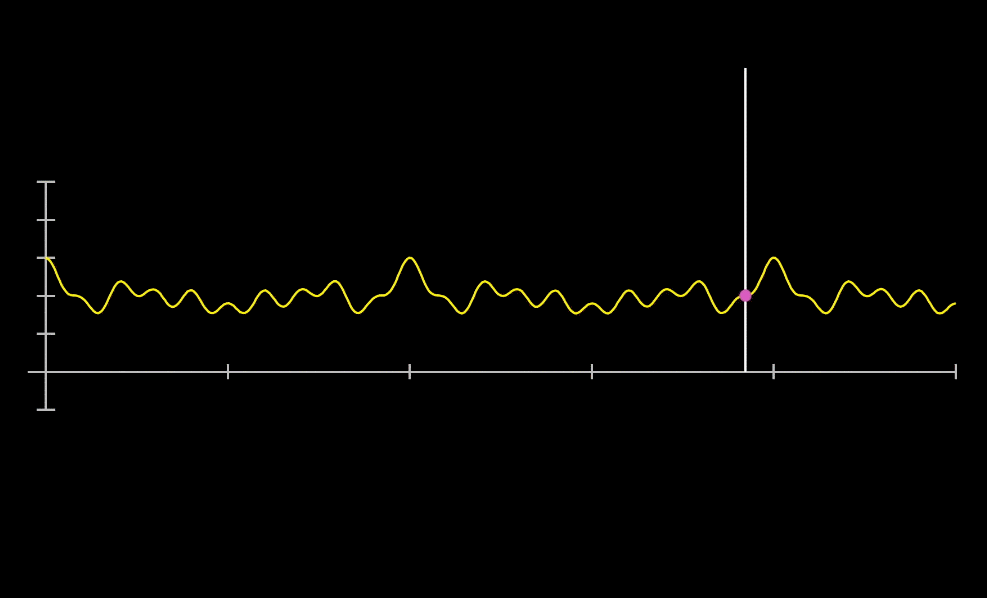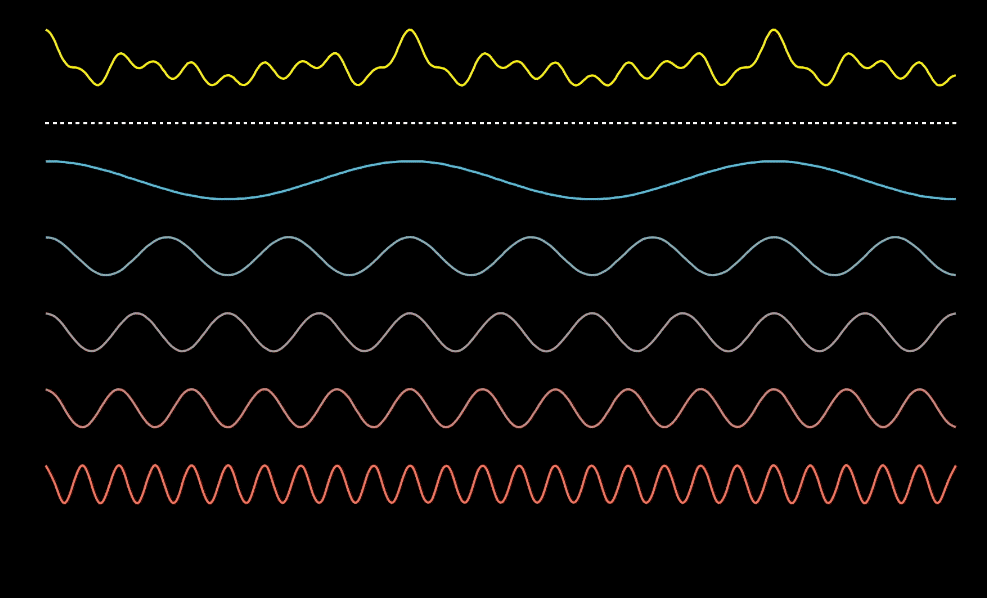
つまり、以下の図のように波形を複数の正弦波に分離することができます。
次に下の図を見てみてください。
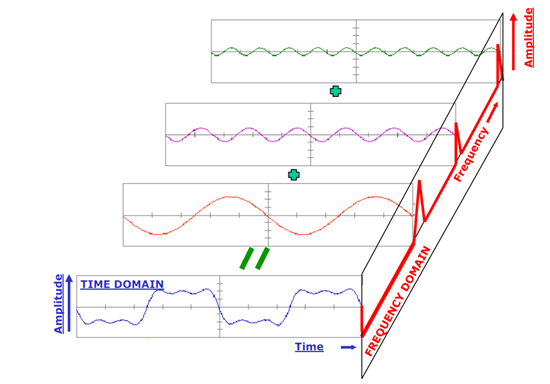
もともとの音声は時間域ですが、このままだと音声の特徴は分かりにくいかもしれません。
フーリエ変換を用いて音声波形を複数の正弦波に分けることができます。
各正弦波の周波数や振幅が分かれば、周波数域で分析ができるため、より音声の特徴が分かりやすくなります。
え・・・音声って分離されるの?
混ざっている絵具から、元の色を分けるみたいでムズイ!
難しいですよね。でも、非常に大切なので覚えてくださいね。
難しい理論でも違う角度みたら何かわかるかもしれません。
それではフーリエ変換を理解するためのキーアイテムを見せましょう。
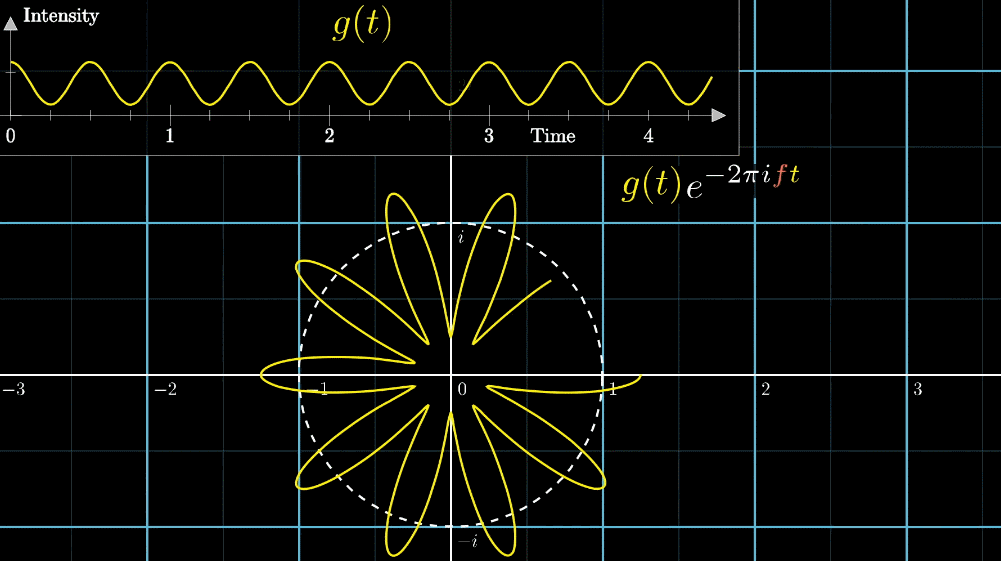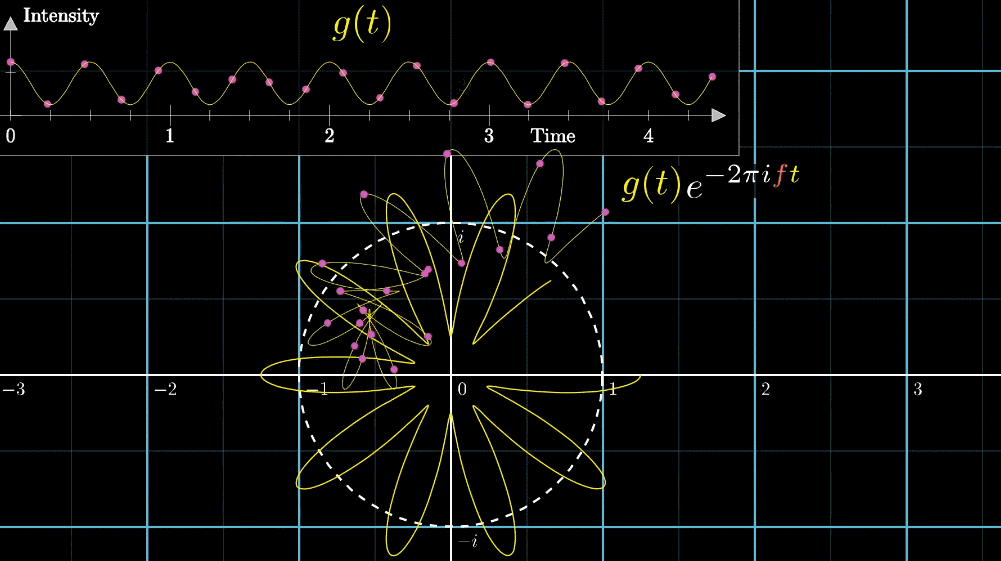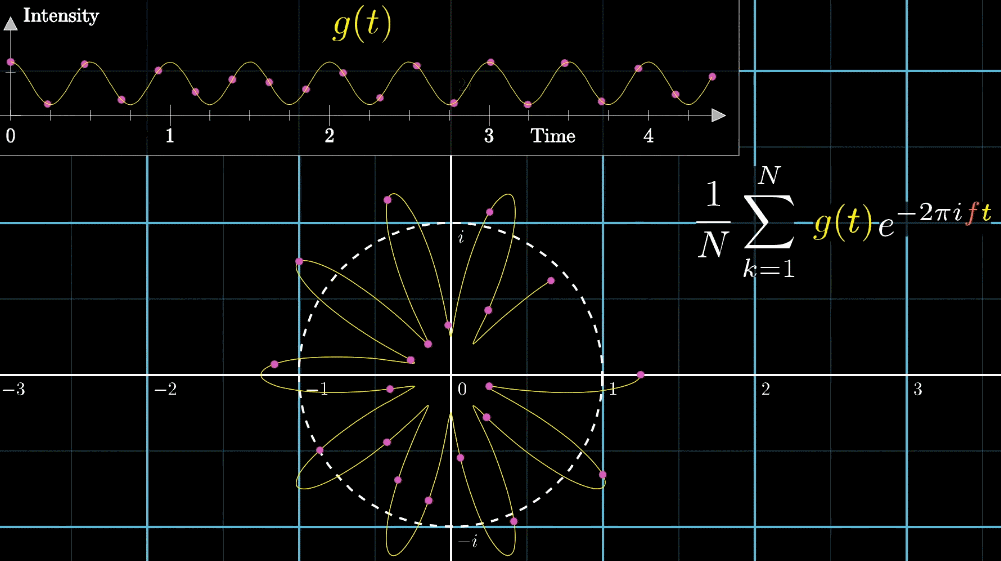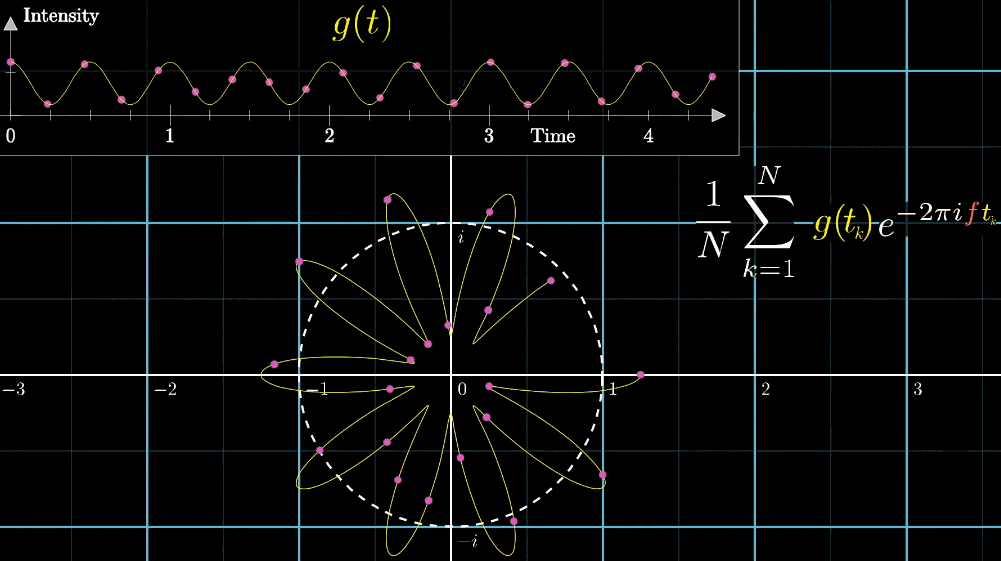
下の図をご覧ください。
上部の波形は1秒に3回振動する波です。
アニメーションのように波形の振幅が原点からの距離となるように下部の座標に配置します。
下部の座標に配置された波形を描くように2秒1周のペースで白矢印が動きます。
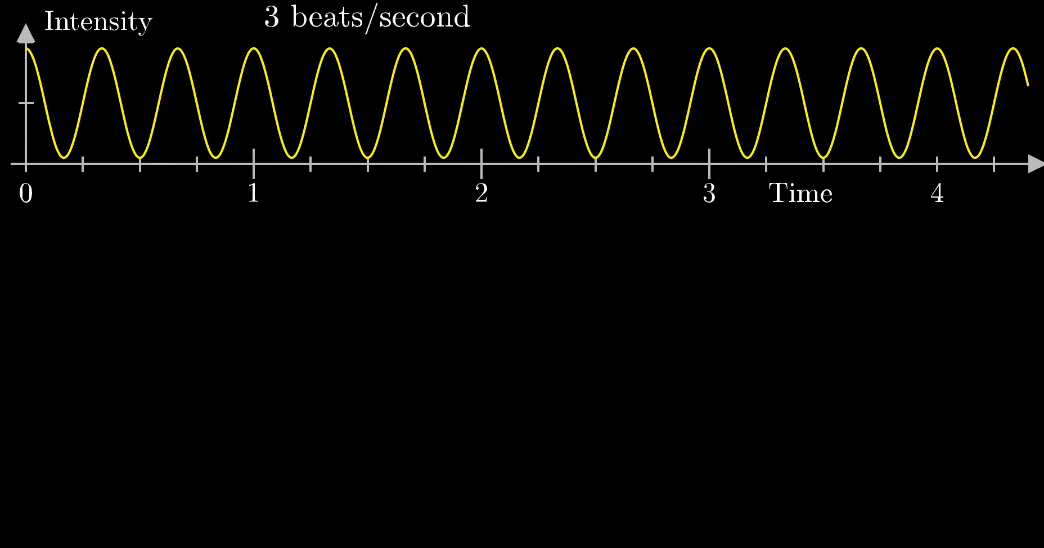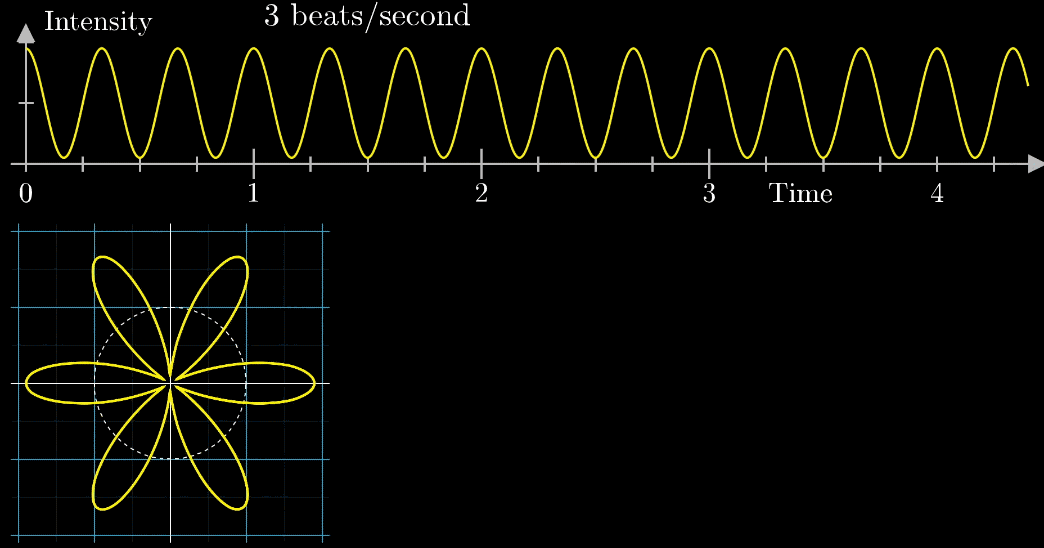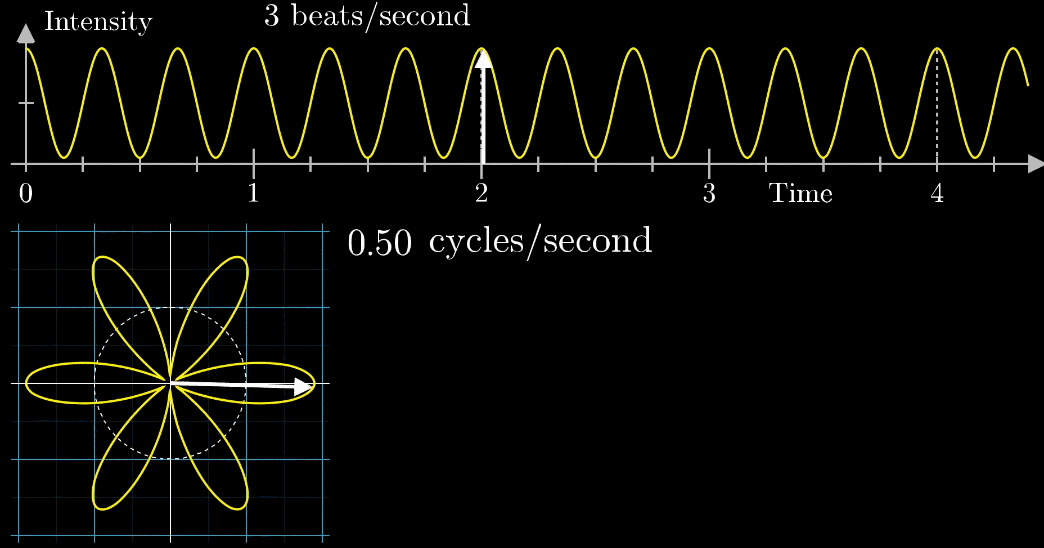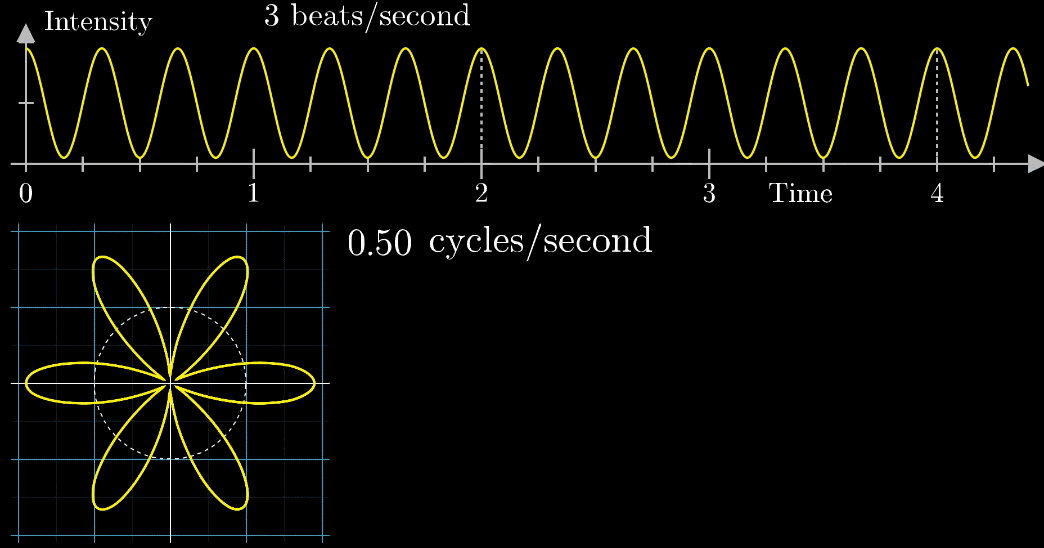
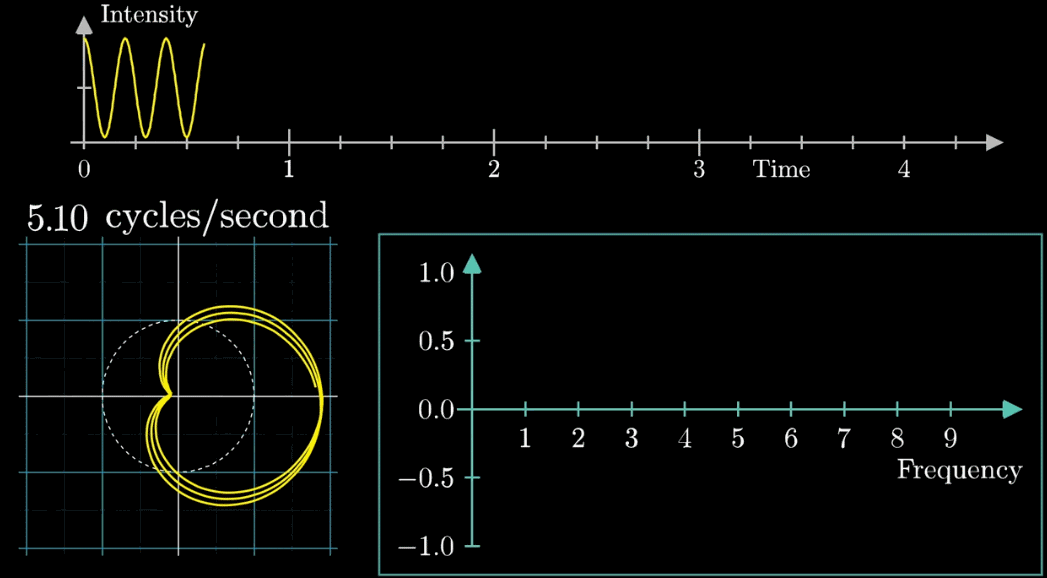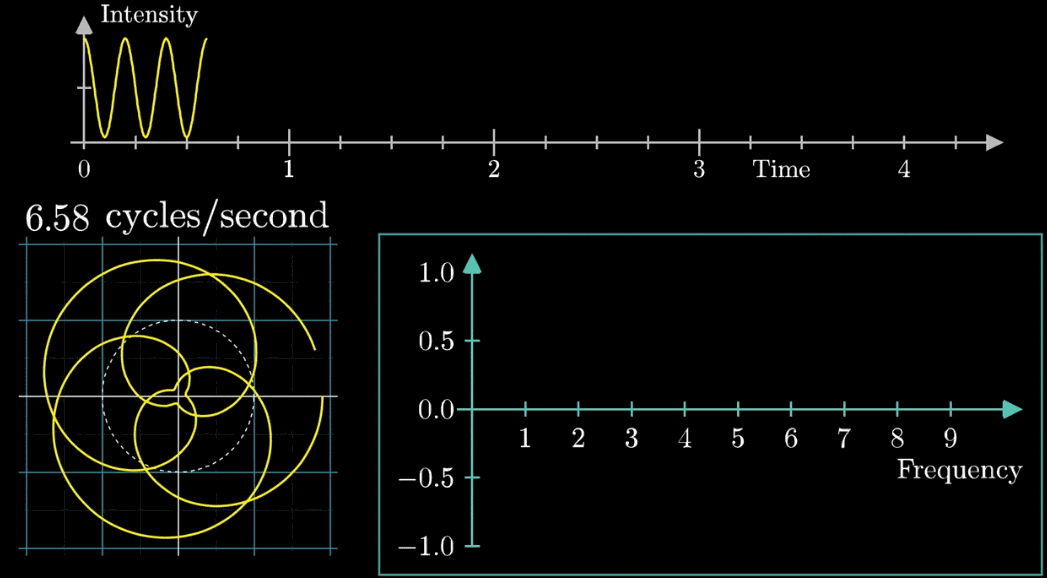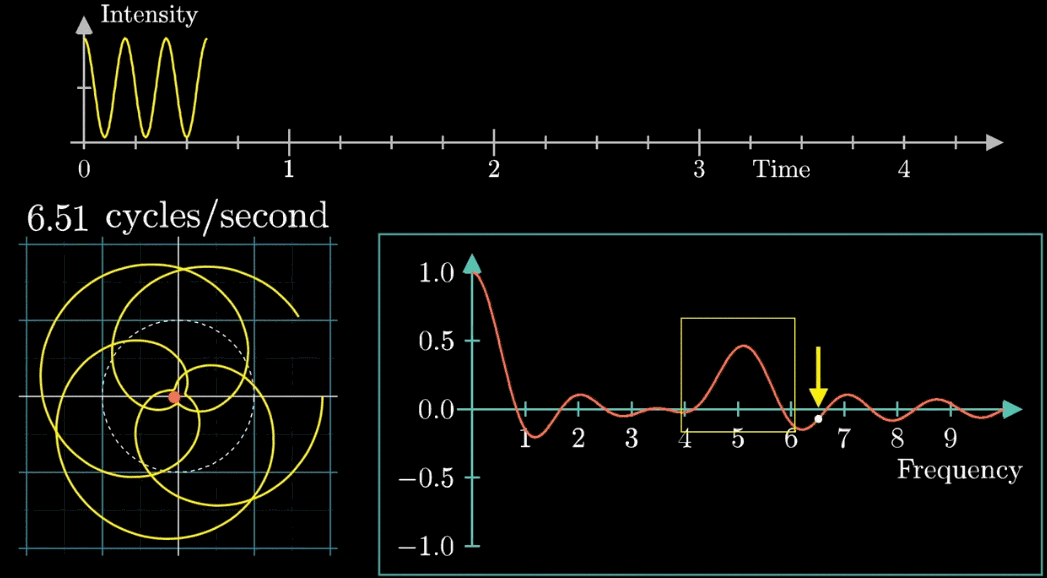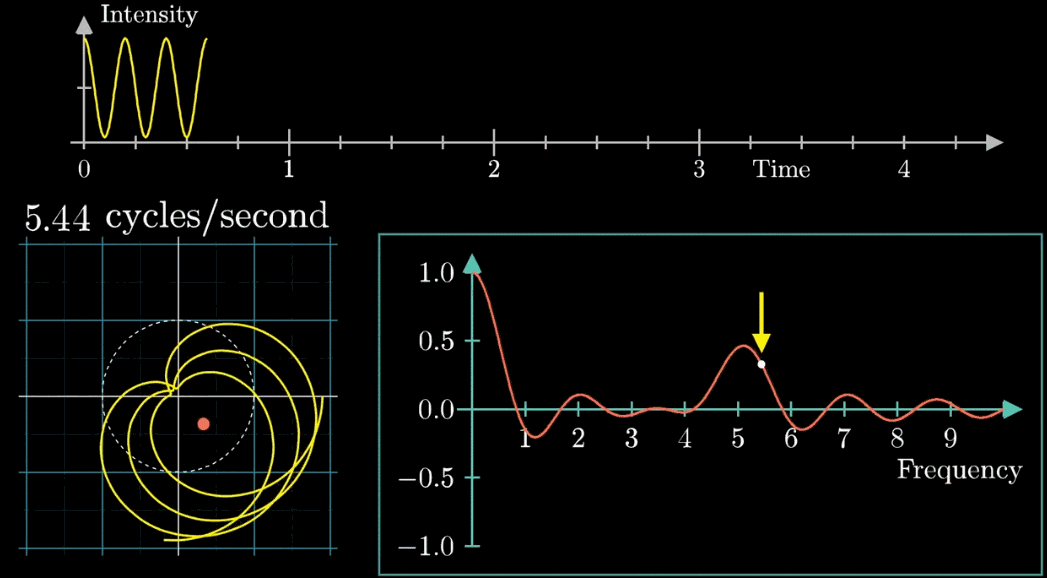
もともと波の周波数(3回/秒)と矢印移動の周波数(0.5周/秒)の2種類の周波数があるね。
矢印の移動の速さが変わったらどうなるの?
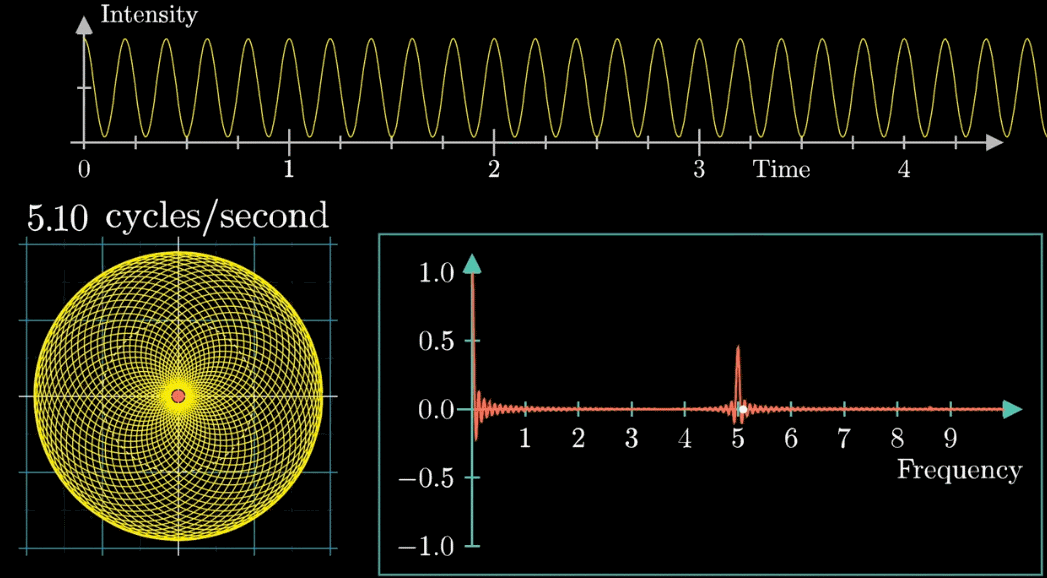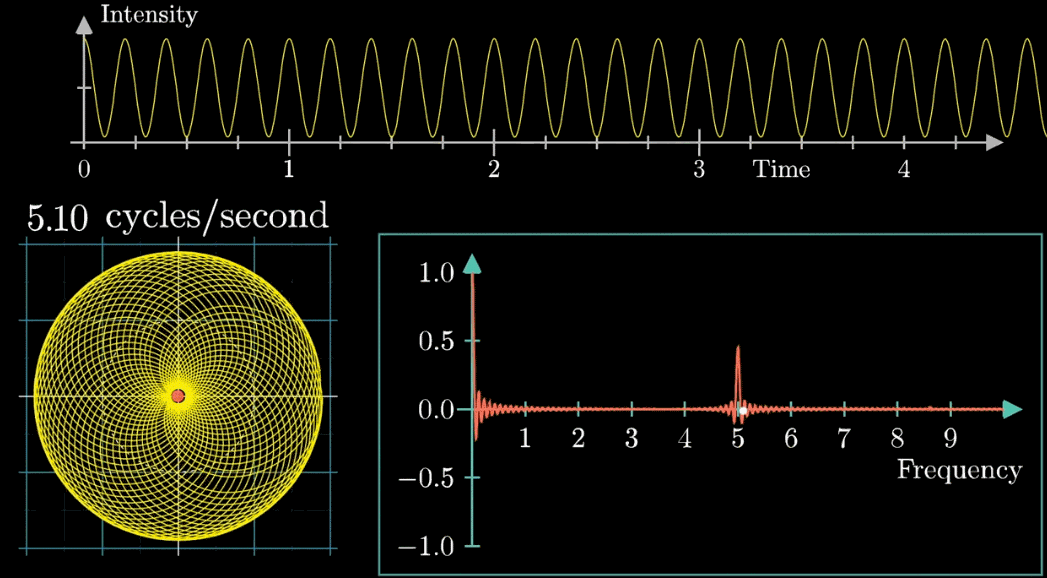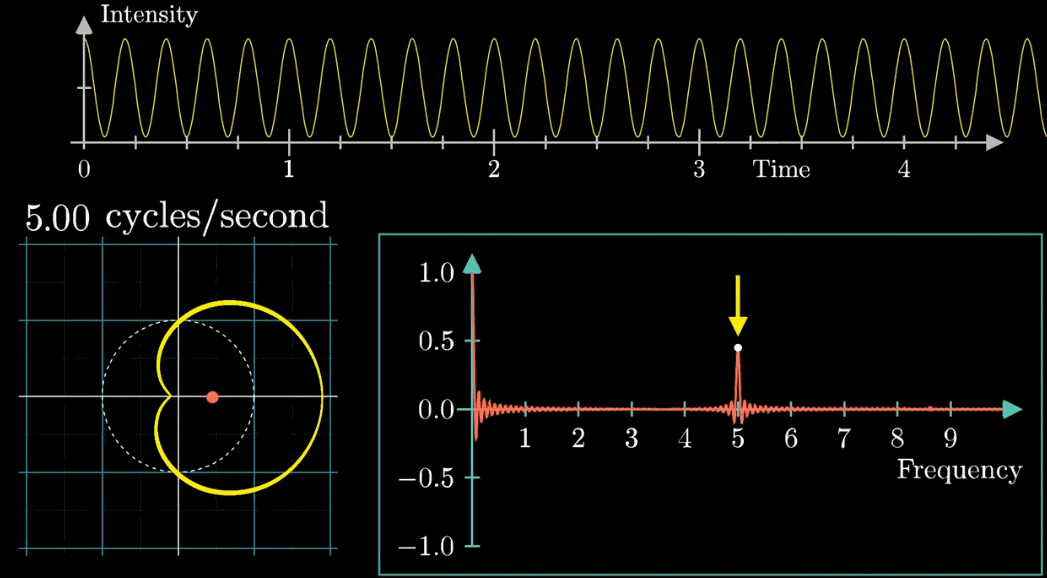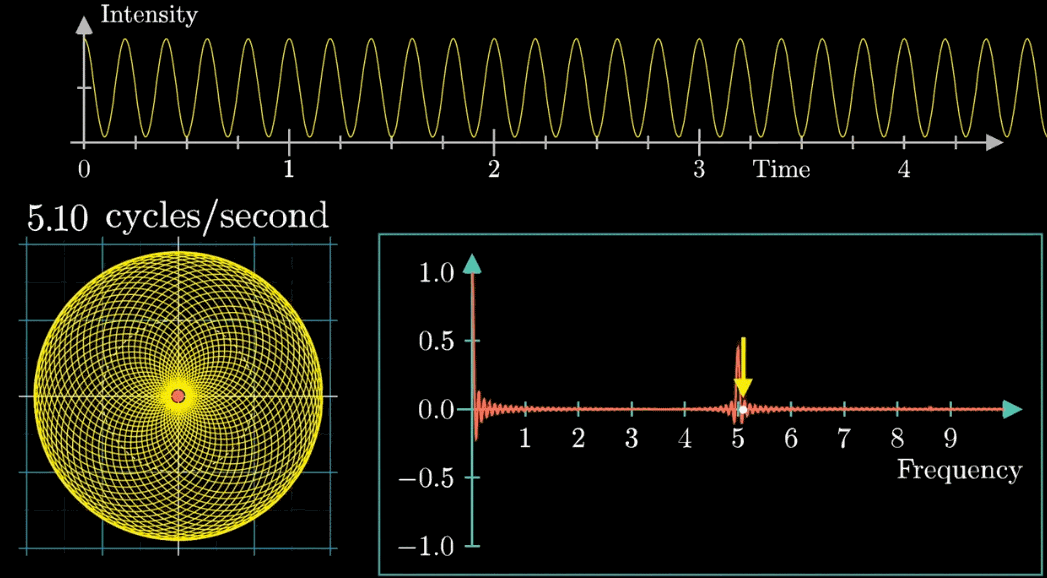
いい質問ですね。下の図を見てみましょう。
この図は矢印移動の速さが変わるときの変化を示したものです。
最初、矢印移動が0.79周/秒から始まり、3周/秒まで段階的に表示します。
矢印移動が3周/秒の時に、安定な軌道となるのが分かります。
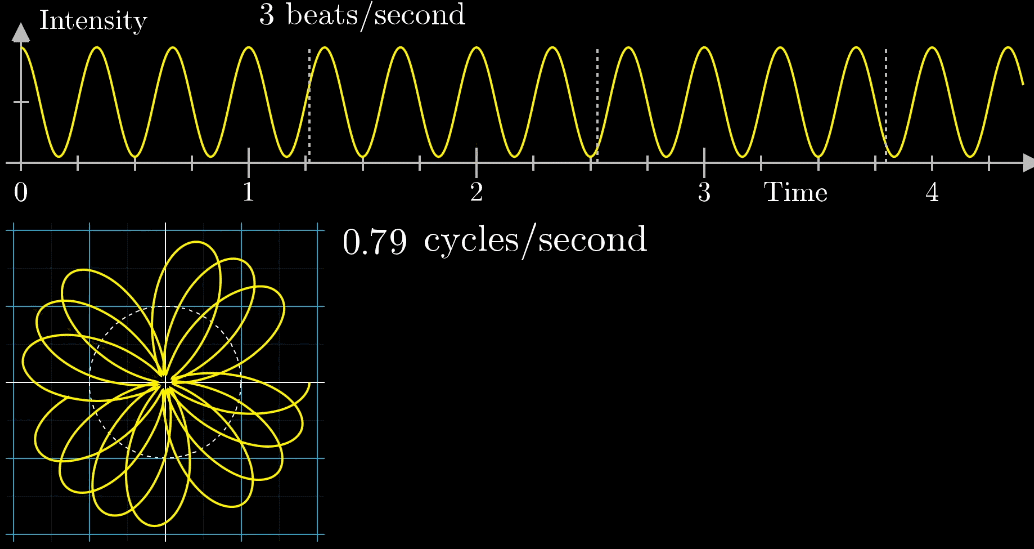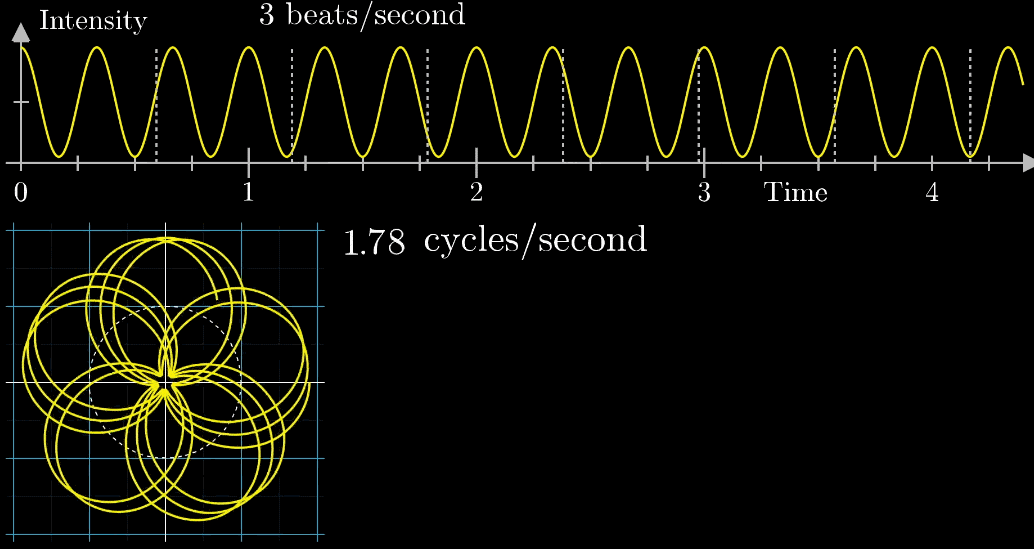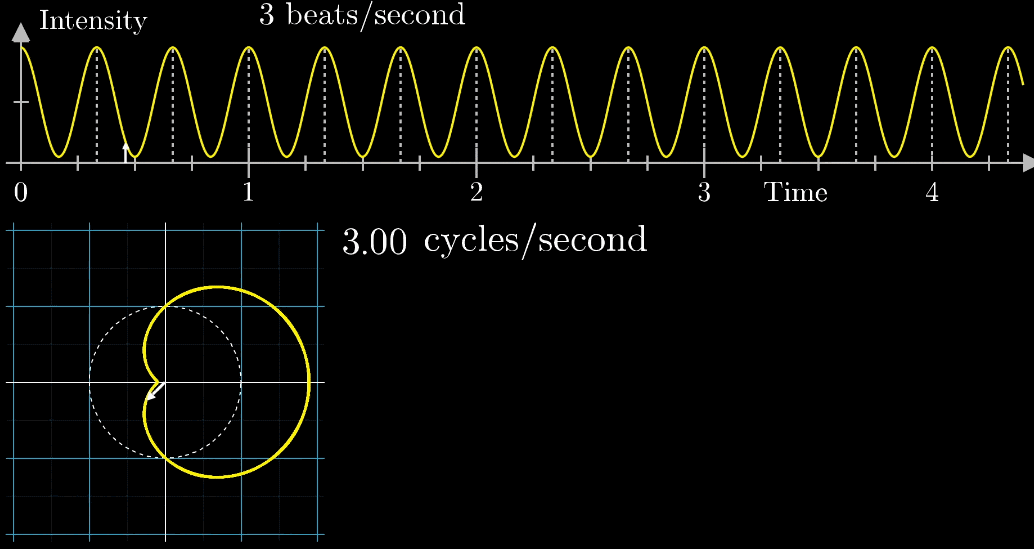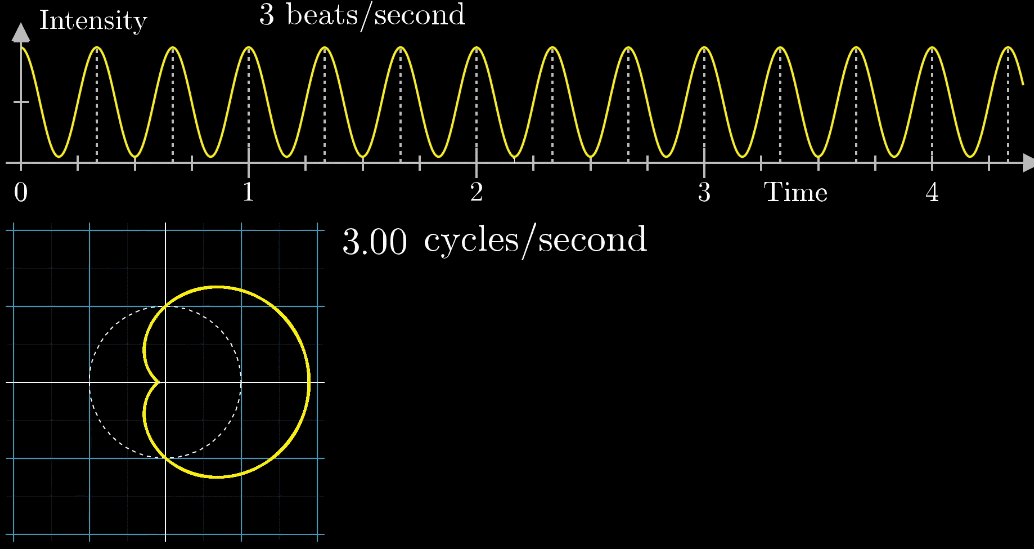
この図はなんだか面白いけど、何ができるの?
入力と出力について考えてみましょう。
この図における入力は矢印移動の速さ、そして出力は矢印の先端が通過した軌道です。
最初の軌道はめちゃくちゃではあるものの、原点に点対称な軌道になります。
矢印移動の速さが3週/秒の時、軌道は安定するものの原点に対して偏った軌道になります。
偏った軌道・・・。
重心を表示すれば何かわかるかな?
いいですね。
それでは、重心を見てみましょう。
先程の図の矢印移動速度を段階的に変更させたときの軌道とその重心の変化を以下の図で示します。
右側の図は矢印移動速度に対する重心の\(x\)成分です
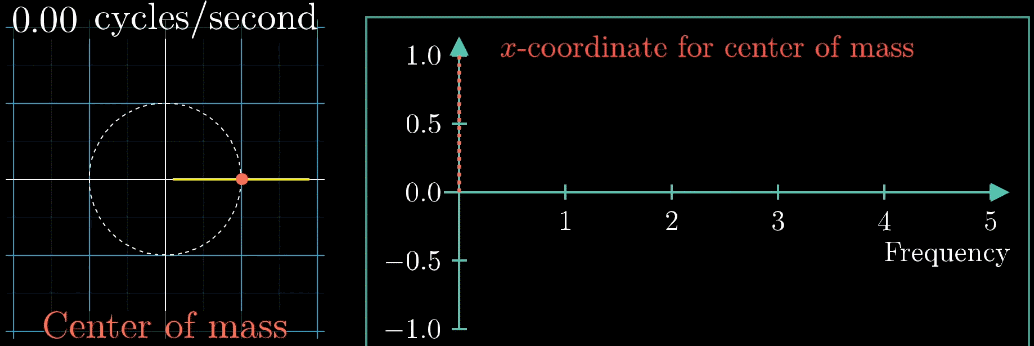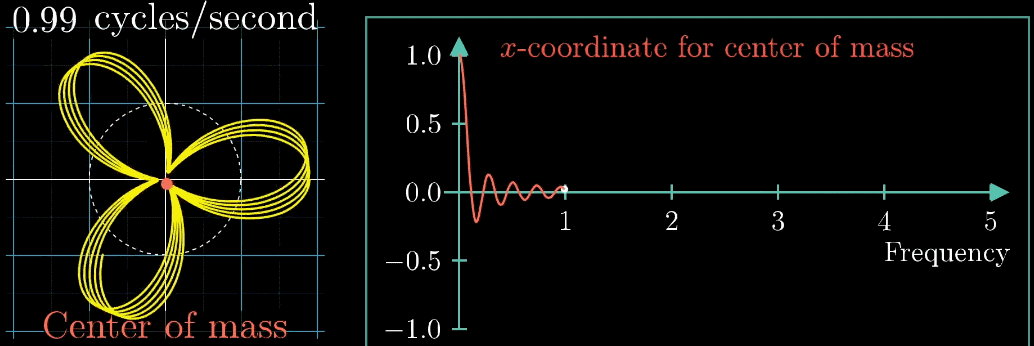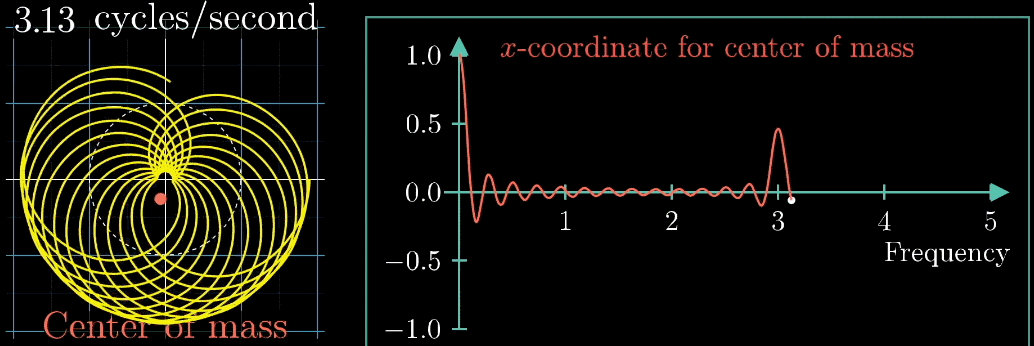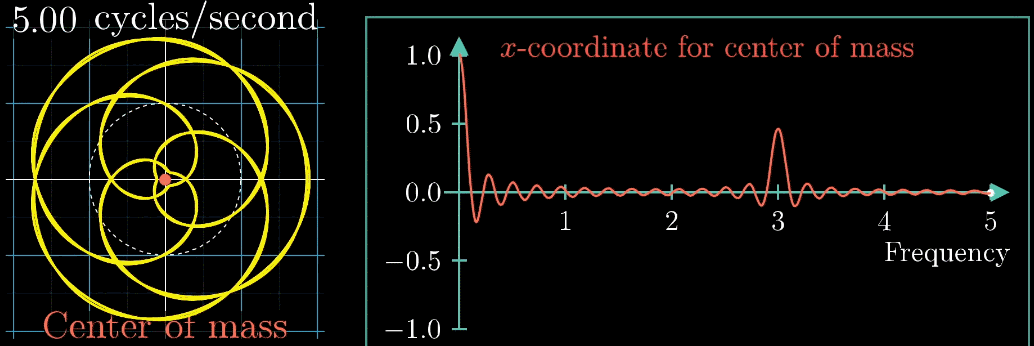
3周/秒の時にパラメータが大きくなってる・・・。
どこかで見たような・・・。
それでは、二つ音声を組み合わせた波形で試してみましょう。
以下の図のようになります。
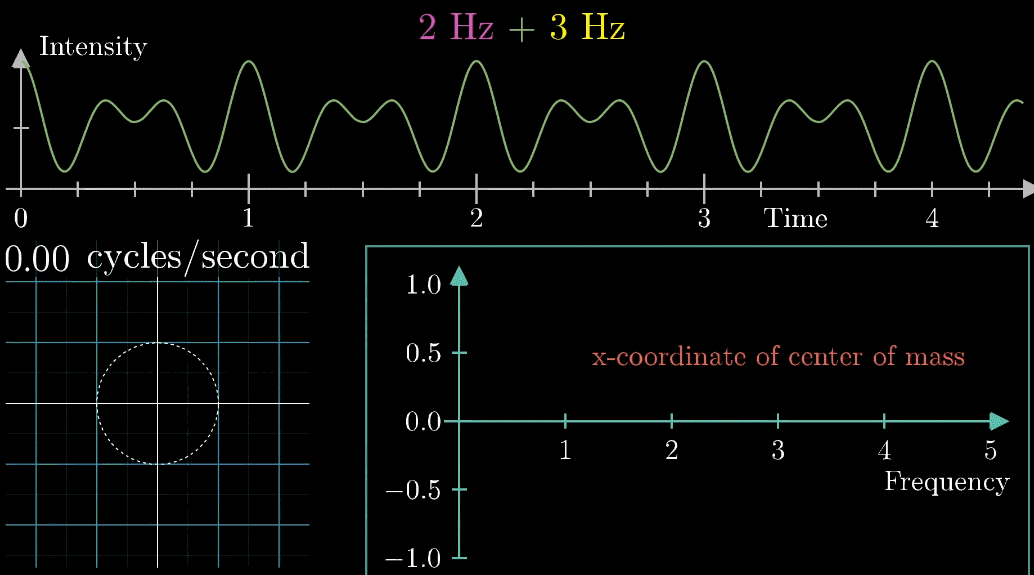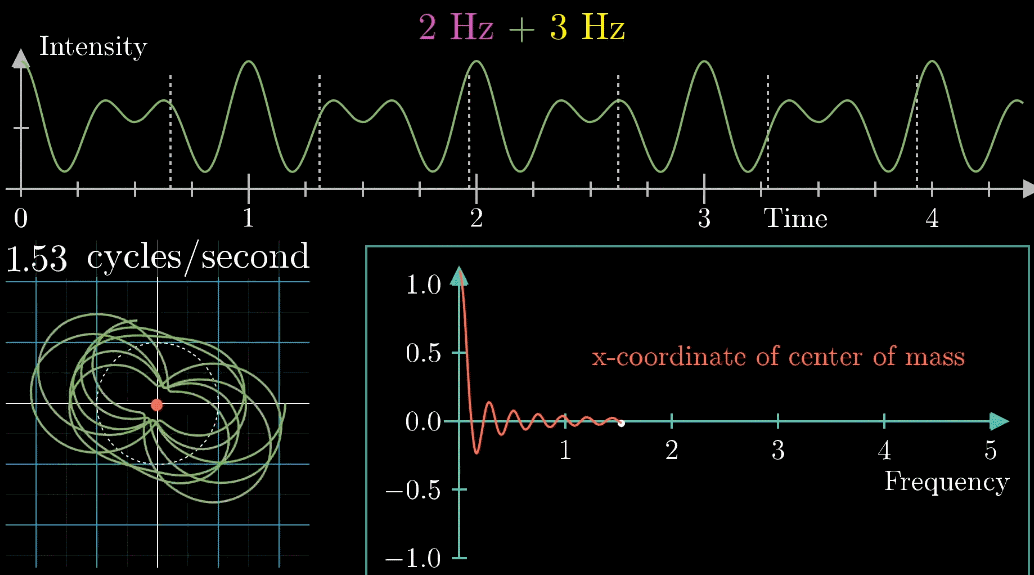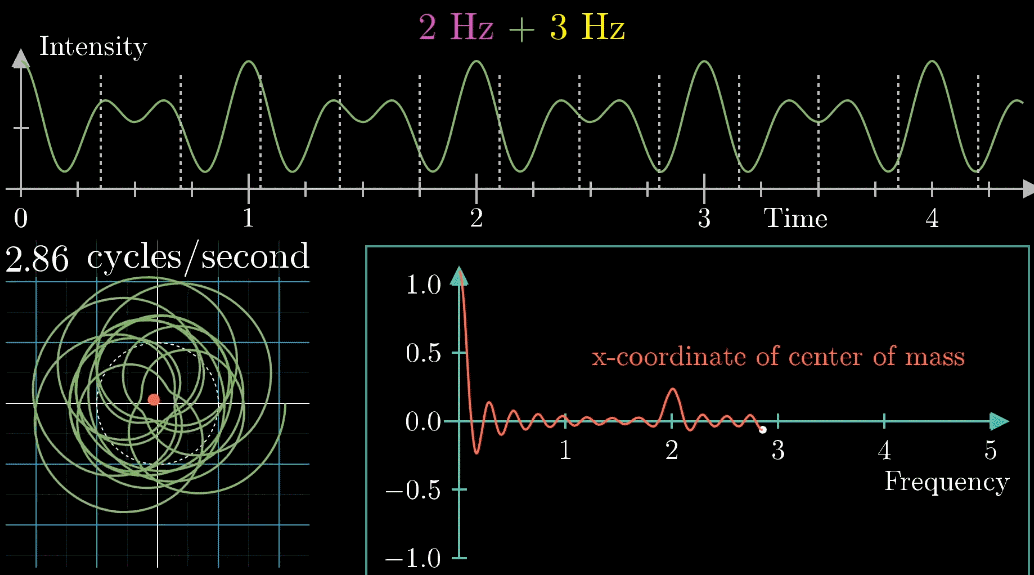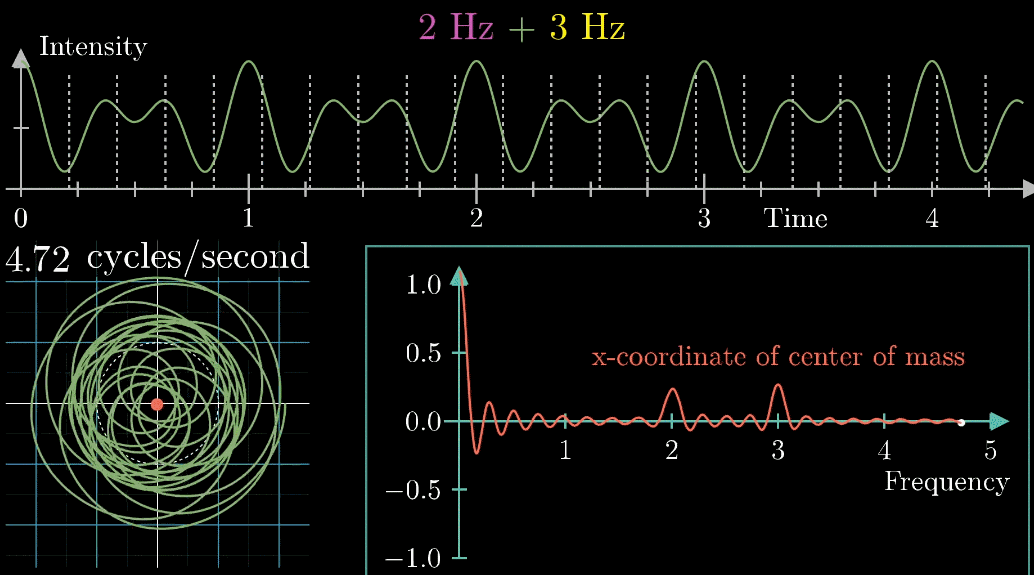
今度は2周/秒の時と3周/秒の時にパラメータが大きくなってる・・・。
これってまさか、フーリエ変換?
よく分かりましたね。
この仕組みで、時間域から周波数域への変換ができます。
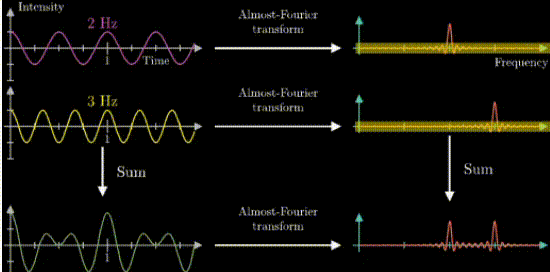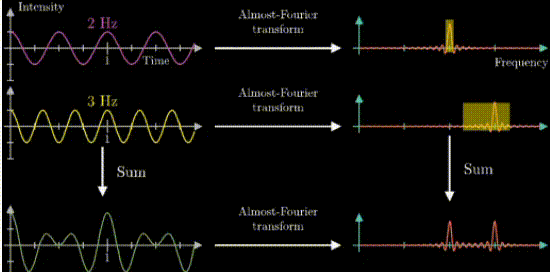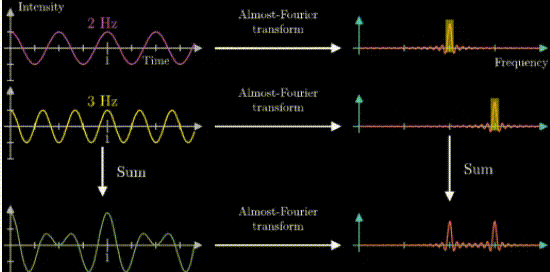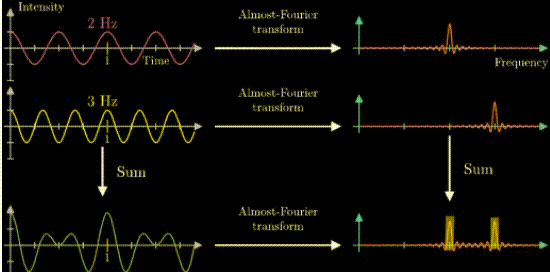
この図は分かりやすい!
でもこれをどうやって数学で表現するの?
まず最初は円の移動です。先程やったの複素平面を使います。
\(e^{2 \pi it}\)は1秒に1周回る円です。
\(t\)に\(f=1/10\)を掛けると、1秒に10分の1周を回る円になります。
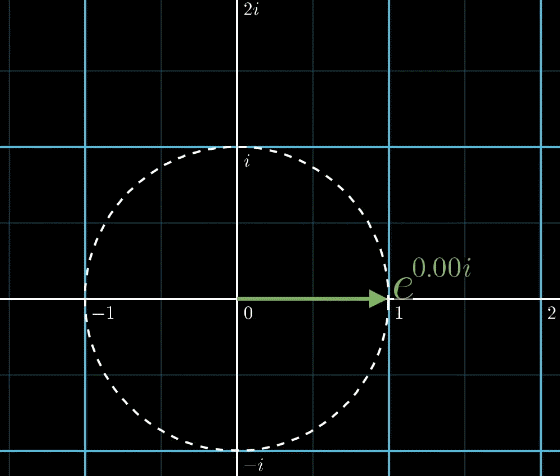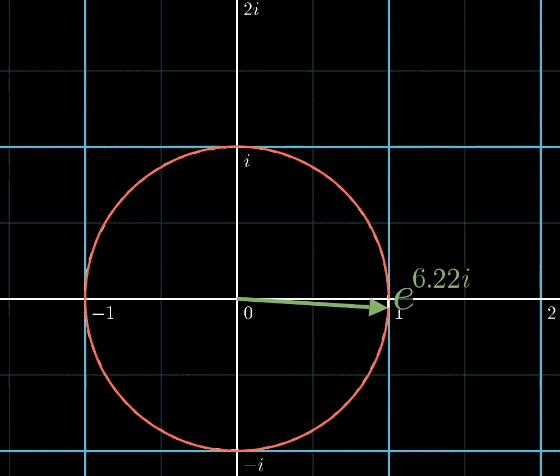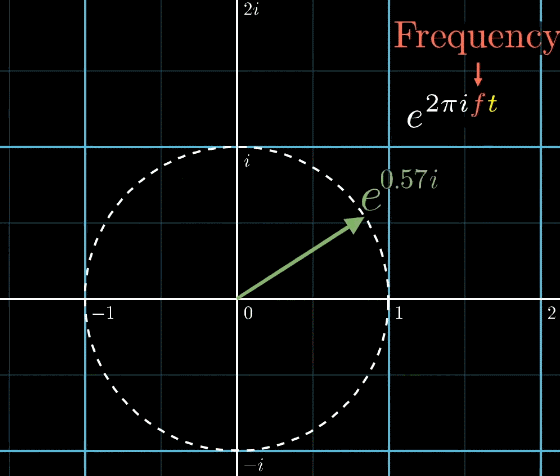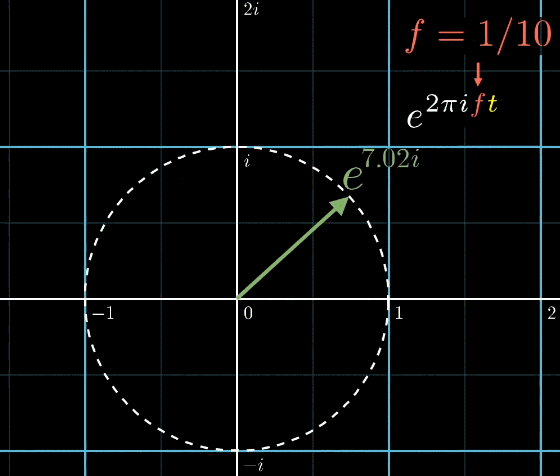
でも、この図は反時計回りで前の図は時計回りだったよ?
よく気が付きましたね。
それなら、\(e^{2 \pi ift}\)の指数に\(-1\)を掛けることで逆回転にすることができます。
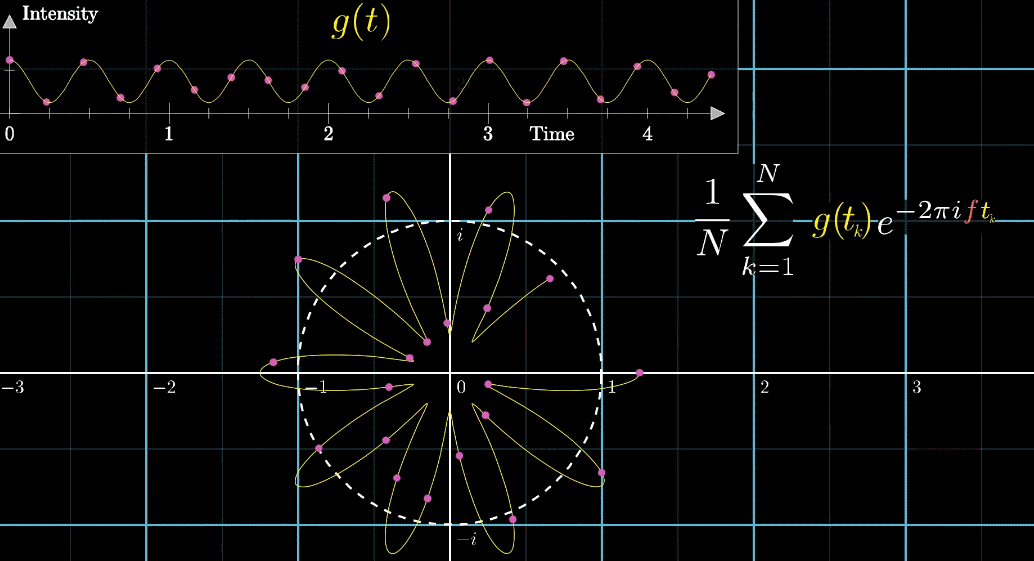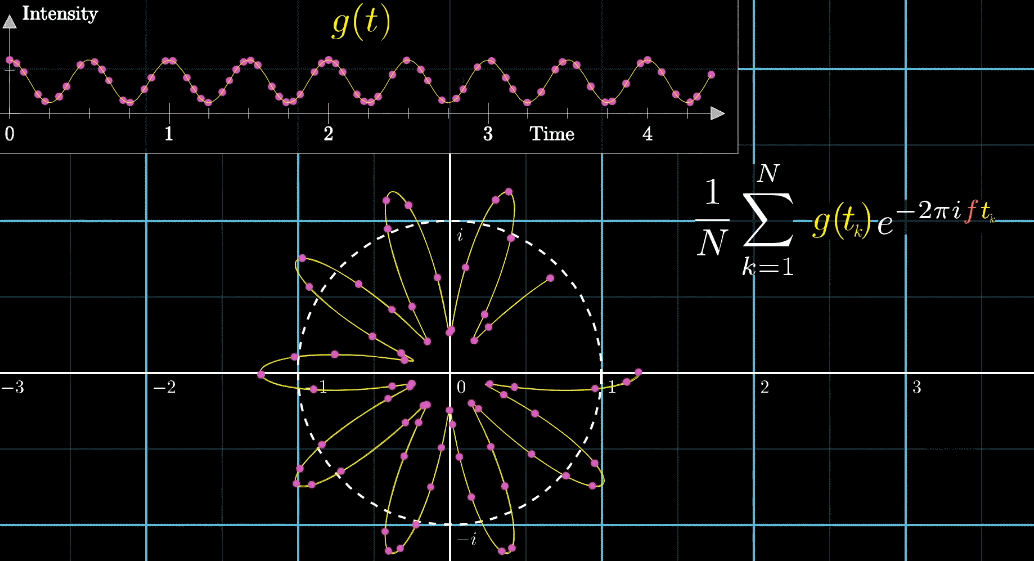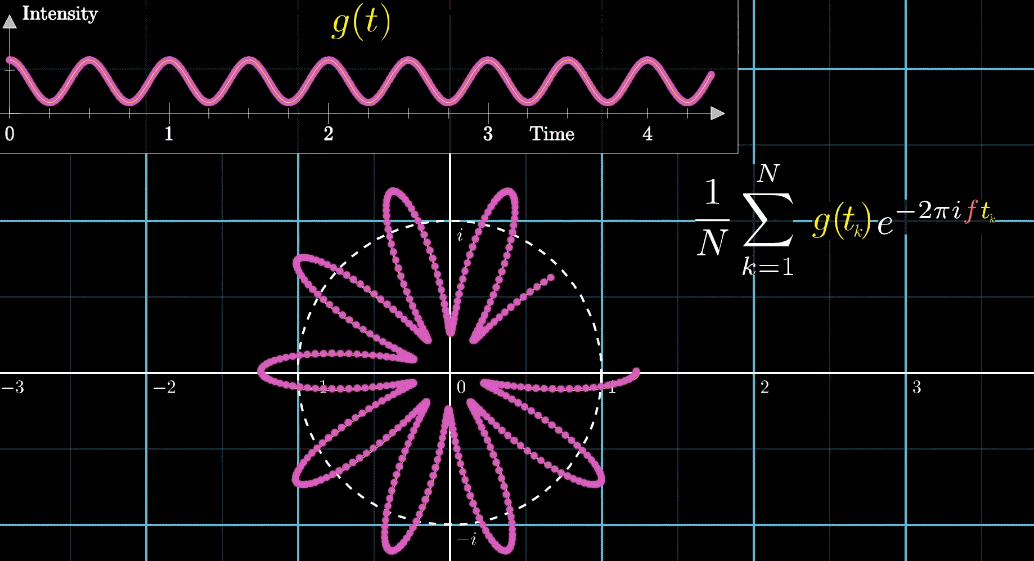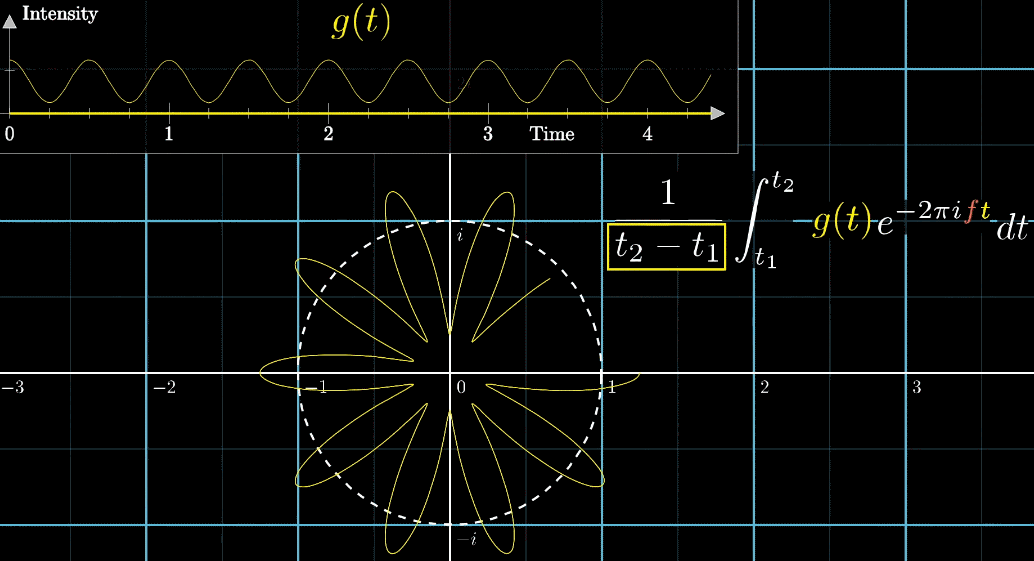
フーリエ変換の対象となる波形を\(g(t)\)とすると、\(g(t)e^{-2 \pi ift}\)で振幅と回転を持つ先程の軌道を描画できるようになります。
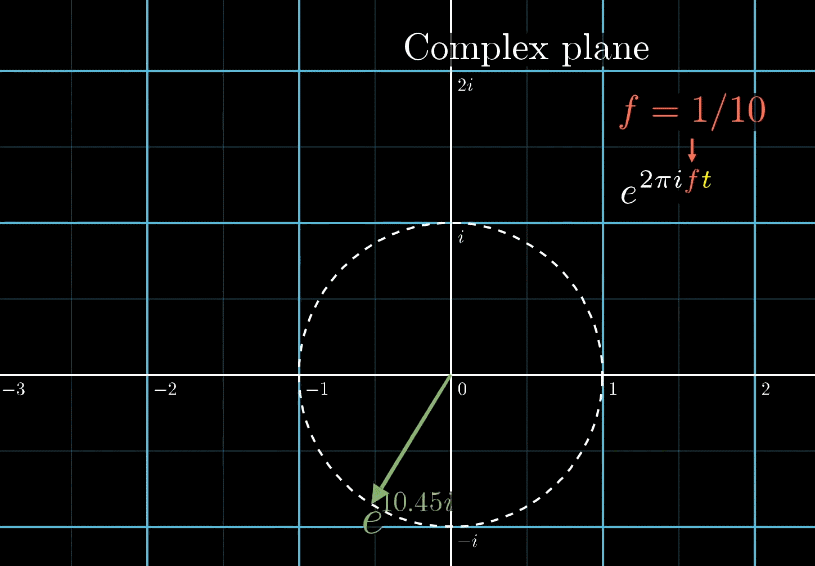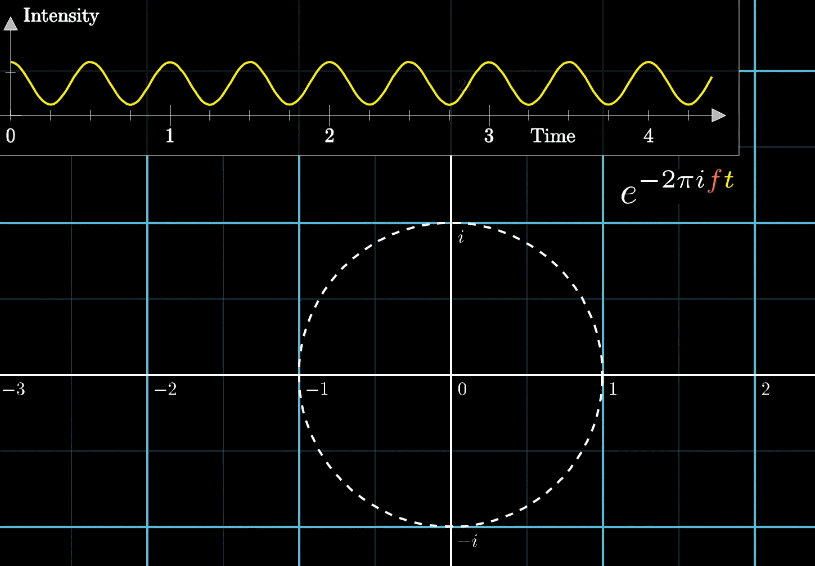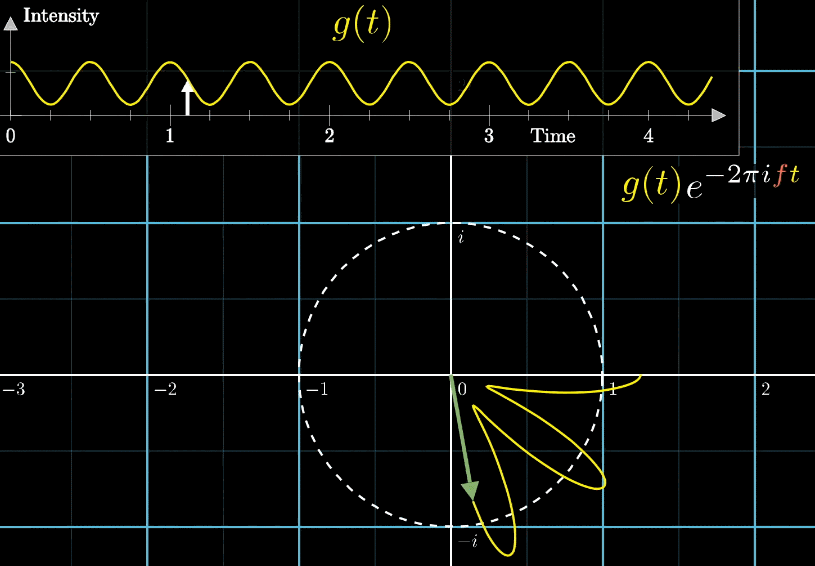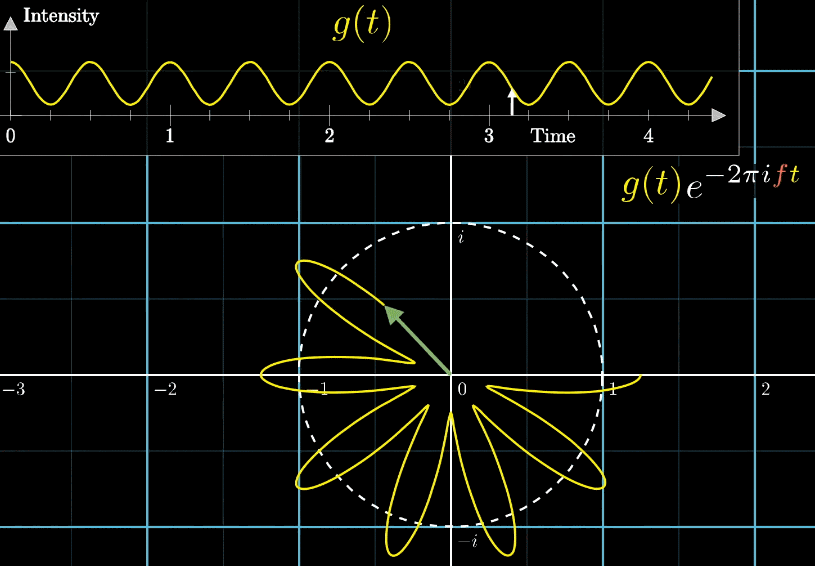
なるほど。次は重心だね。
そのとおり。重心は簡単です。
正方形の重心は辺の上を等間隔で\(n\)個点を取って、その平均値を計算します。
波形においても同様に、\(N\)個のサンプル点を取って平均値を計算します。
式で書くと\(\frac{1}{N} \sum_{k=1}^{N} g(t_{k}) e^{-2 \pi i f t_{k}}\)のようになります。
サンプル数が増える場合、積分関数を使って、\(\frac{1}{t_{2}-t_{1}} \int^{t_{2}}_{t_{1}} g(t) e^{-2 \pi ift} dt\)のように表します。
前言ってたフーリエ変換公式\(\hat{f}(\xi) = \int^{\infty}_{-\infty} f(x) e^{-2 \pi i x \xi} dx\)に似てるね。
そのとおりです。
上の重心を算出する式において、係数\(\frac{1}{t_2-t_1}\)を取り除いた関数を\(\hat{g}(f)\)とすると、積分範囲は異なりますがフーリエ変換と同じような式\(\hat{g}(f) = \int^{t_{2}}_{t_{1}} g(t) e^{-2 \pi ift} dt\)を得ることができます。
係数\(\frac{1}{t_2-t_1}\)は波形の長さに応じて変化する原点から重心までの距離を算出する倍数です。
この係数を取り除いた\(\hat{g}(f)\)は原点と重心の延長線上に存在する点を意味しており、信号が長いほど、値が大きい。
例えば、3秒の波形なら原点・重心位置間の3倍、6秒の波形なら原点・重心位置間の6倍の値が出力されます。
これにはどんなメリットがあるの?
後で説明しますが、波形の長さが長いほどフーリエ変換を行ったとき、周波数域が波形の周波数成分に集中しやすくなります。
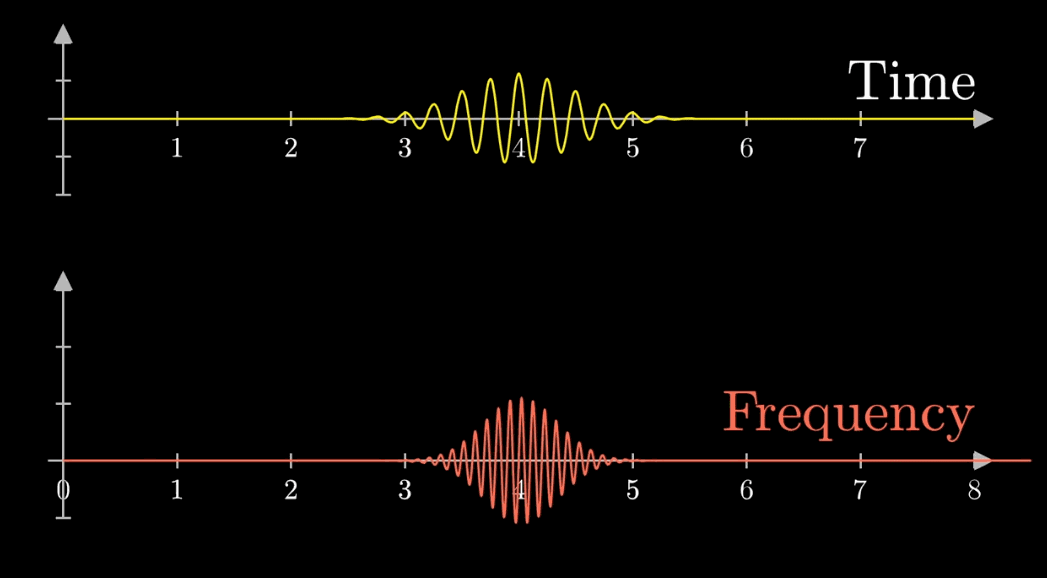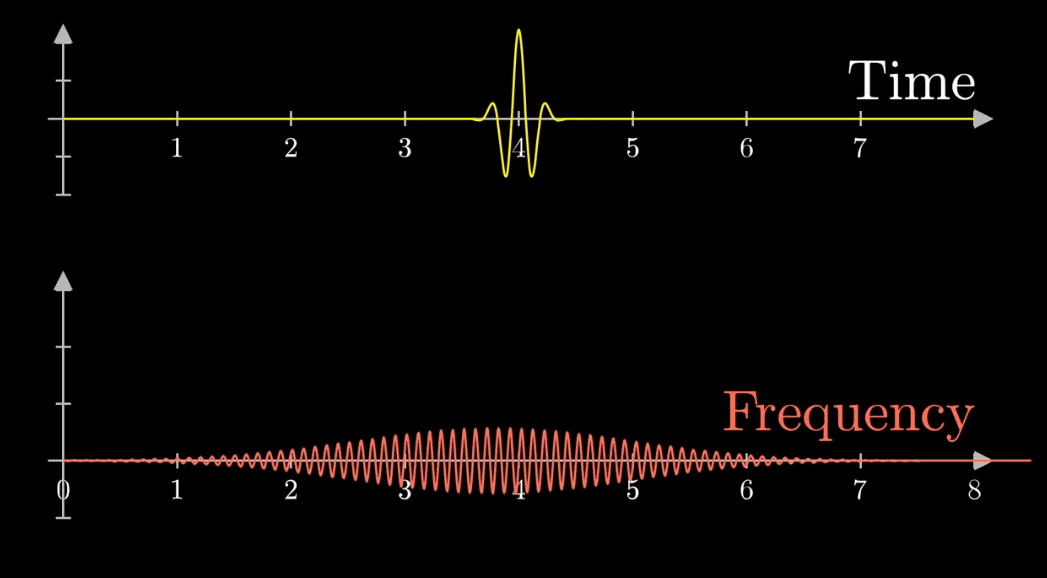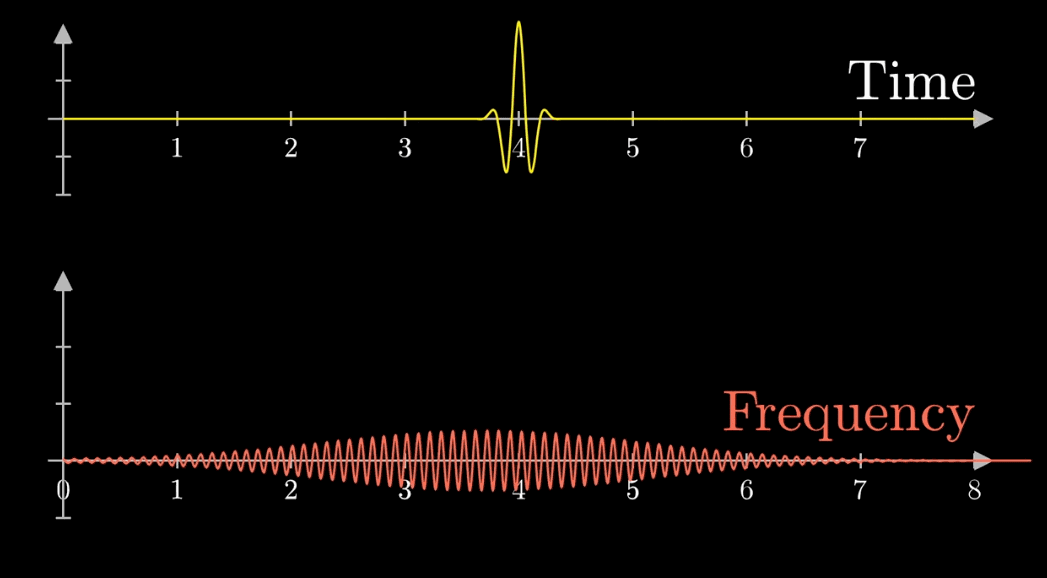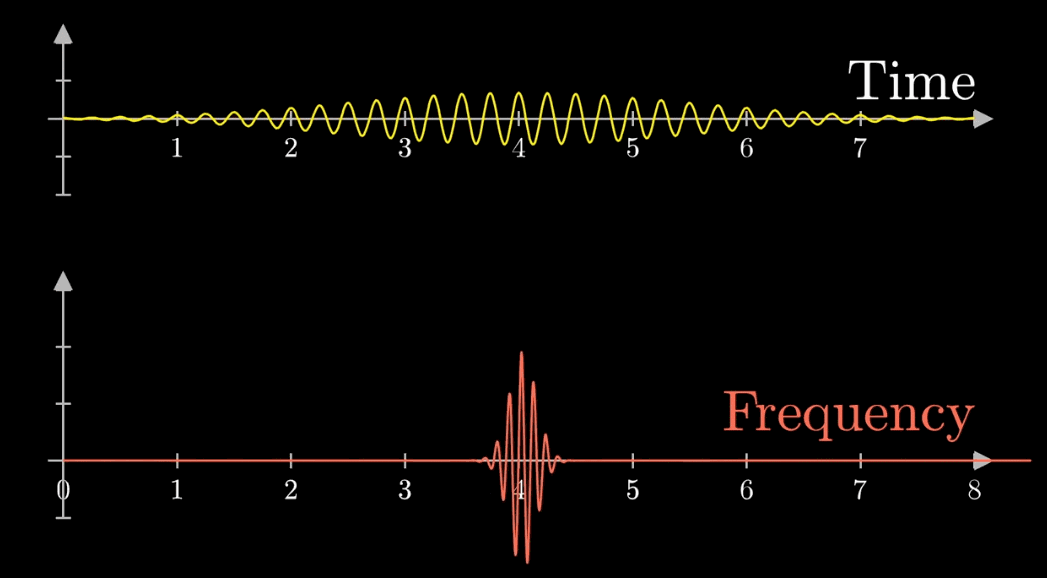
\(\hat{g}(f)\)は積分範囲が有限ですが、実際のフーリエ変換の積分範囲は無限だよね。
これにはどんな意味があるの?
積分範囲が無限なら下の図のように、周波数域が波形の周波数成分の位置でのみ存在するようになります。
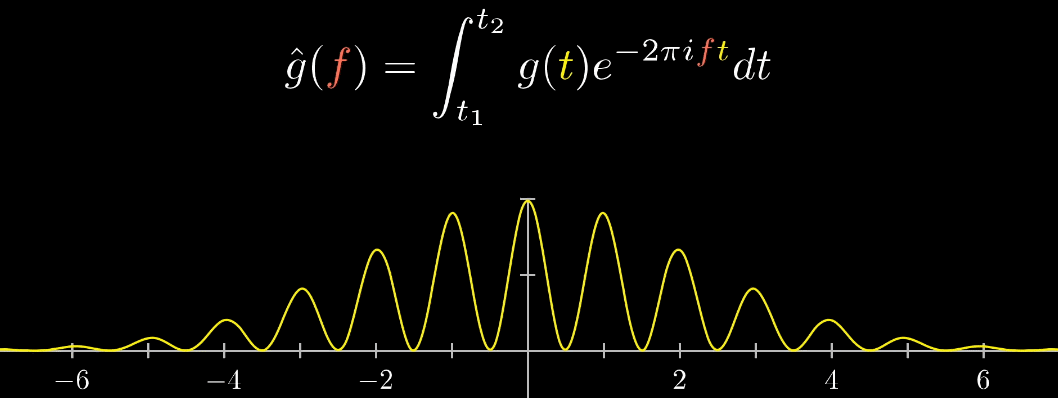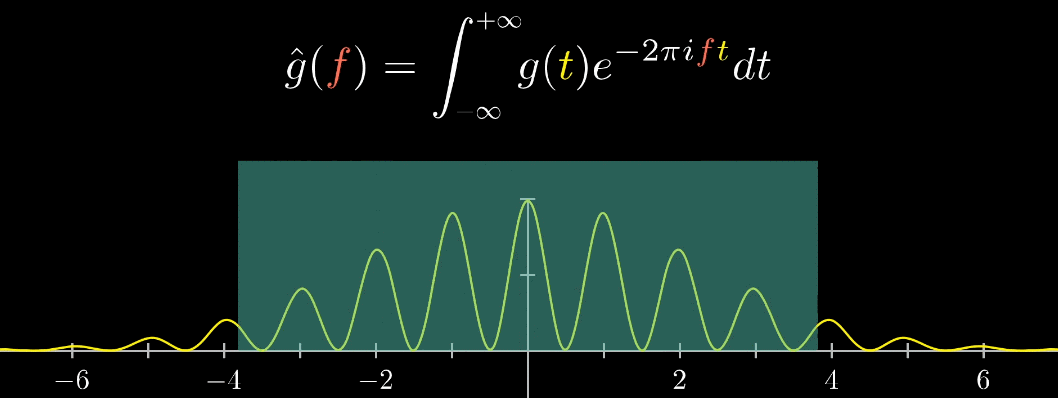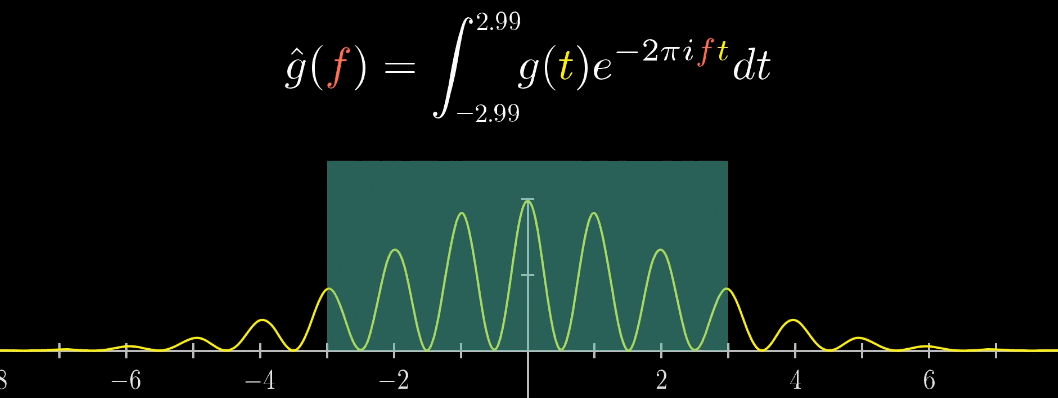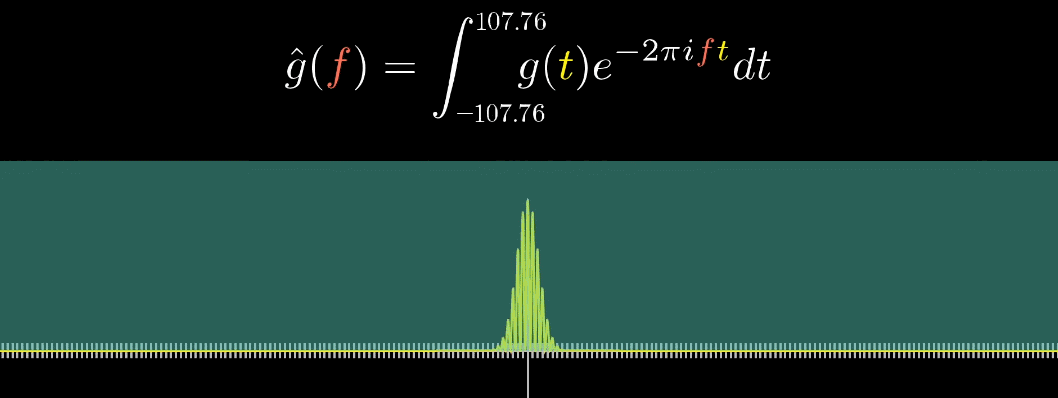
信号の長さとフーリエ変換は関係あるの?
あります。
信号長い場合、下の左側の図のように円の周りの線が多く、その重心が原点に近づくスピードは速くなります。
信号が短くなると、右側の図のように重心が原点に近づくスピードが遅くなります。
上記のように信号の周期が長いほど、周波数域は集中します。
そのため周期性の情報を抽出しやすくなります。
なるほど、フーリエ変換はわかった気がする。
それじゃあ、短時間フーリエ変換(STFT)は?
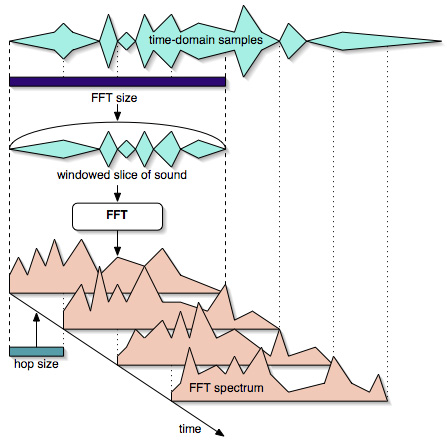
STFTとは、音声波形に対して窓関数をずらしながらかけ、窓関数で切り取られた区間それぞれをフーリエ変換することです。
フーリエ変換は公式では無限ですが、実際の波形を処理する際は区切らなければいけません。下の図は窓関数をずらしながら波形を切り取り、周波数成分を抽出しているSTFTのイメージです。
でも、具体的にはどんな時にSTFTを使うの?
実際の音声は、時間よって周波数成分が変化します。
フーリエ変換では音声の時間的な変化をうまく表現することができません。
STFTは、音声信号をある短い時間で分割しフーリエ変換をすることで、時間的に変化する信号の周波数成分を表現できるようになります。
STFTはノイズ削減・ピッチ検出・ピッチシフトなどの音声変換の効果を確認する際等、音声の応用分野でよく使われています。
なるほど!
STFTって何なのか分かった気がする!
魏さん、ありがとうございます!
※フーリエ変換の説明として下記動画の一部を使用させていただきました。
英語の動画ですが非常に分かりやすい内容なので、理解を深めたい方は是非ご覧ください!