基本周波数について

こんにちは、Hmcomm RD2チームの佐藤と冨永です。
この度Hmcommでは技術ブログを始めることとなりまして、第一弾記事を我々2人で担当させていただきます。
今回は『基本周波数』について解説します。

目次

• 音の解析の初歩
  • 手法1. 音声波形を可視化する
  • 手法2. 周波数解析をする
• 基本周波数とは
  • 基本周波数が分かると何が嬉しいのか？
  • 実際の音から基本周波数を推定してみる

音の解析の初歩

基本周波数の説明する前に、まずはこちらの２つの音声を聞いてみてください。

つづいてこちらの音声も

Sample A1とA2、 B1とB2は似た様な音の高さに、また SampleA1とB1、A2とB2は似た様な響きに聞こえたかと思います。
これらの音が似ているということを科学的に確認するにはどの様にすればよいでしょうか？

手法1. 音声波形を可視化する

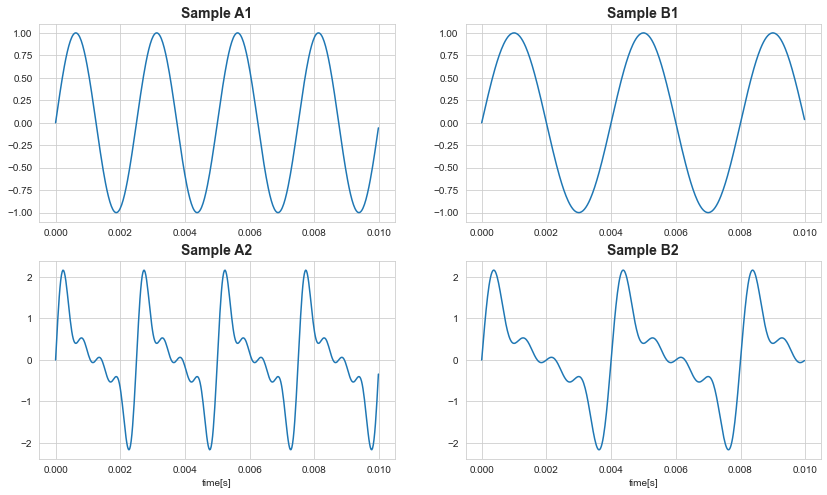
音の解析において『今自分が聞いている音がどの様な波形をしているのか』を知ることは重要なことと思います。
音声波形を見ると、なるほどA1とB1はどちらも単純な波形(正弦波)に、それに比較してA2とB2は少し複雑な波形をしていることが分かります。
響きが似ている理由は波形である程度説明できそうですね。
では音の高さが似ている理由はどの様に説明をするのが良いでしょうか？

手法2. 周波数解析をする

複雑な波形を解析する手法として「フーリエ変換」があります。
「フーリエ変換」の詳しい解説は今後社内の誰かがブログに起こしてくれると信じて、ここでは「フーリエ変換とは波形を単純な波(正弦波)に分解する変換である」という説明に留めたいと思います。
では今回の音をフーリエ変換するとどの様になるでしょうか？

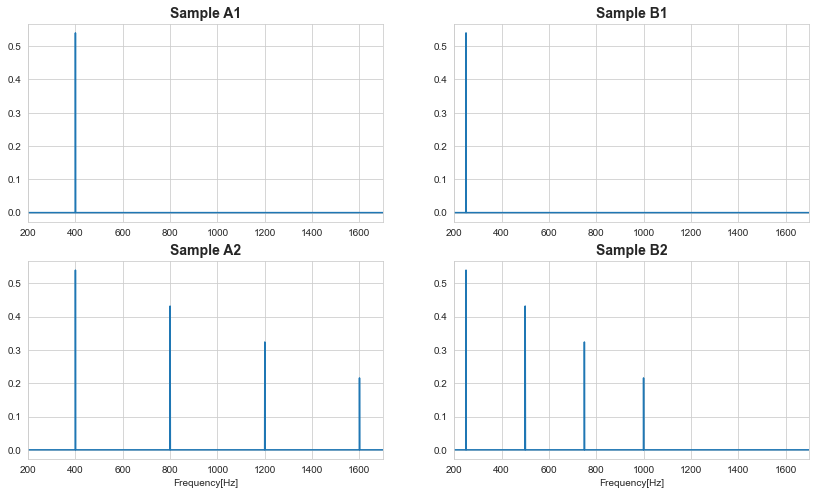
この図では波の周波数スペクトルを表現しています。
つまり、横軸が周波数で縦軸がエネルギーの大きさの図で、元の波に各周波数の成分がどれだけ含まれているかを確認できます。
ちなみに周波数とは『1秒間に波が振動する回数』を表す単位であり、例えば400Hzであれば1秒間に400回振動する波となります。周波数の大きさが耳で聞いた時の音の高さに影響します。

A1とB1はそもそもが単純な波であったので、フーリエ変換でそれぞれ周波数400Hzと250Hzの成分のみが含まれていることを確認できます。
複雑そうに見えたA2とB2も実は4つの周波数の波の足しあわせで表現できることが分かりますね。

基本周波数とは

前置きが長くなりましたが基本周波数とは、
『その信号に含まれる周波数成分で最も周波数の低いもの』
と定義され、基本周波数の大きさは音の高さの感じ方に大きく影響します。
改めて周波数スペクトルの図を見てみるとA1とA2、B1とB2は基本周波数が一致していることが分かります。

またA2とB2には基本周波数を2,3,4倍にした周波数成分が含まれますが、基本周波数を約整数倍した成分を倍音と呼びます。
ギターやフルートなどの楽器、また人の声などで同じ音の高さでも響きが違って聞こえるのはこの倍音の含まれ方が大きく影響しています。

基本周波数が分かると何が嬉しいのか？

性差または同性でも個人個人で声帯の造りは少しずつ異なりますが、この違いは発声時の音の高さや音色に現れます。
音の高さと密接に関係する基本周波数は、これらの違いを把握するのに重要な特徴となるため、話者認識に利用されます。
また、音の高さは単語のアクセントやイントネーションにも現れますが、このことから音声認識を行う上でも基本周波数は重要な特徴となります。
同様の理由で音声を造り出す合成音声に置いても基本周波数は重要な要素であると理解いただけるかと思います。

実際の音から基本周波数を推定してみる

最後に実際の楽器の音から基本周波数を推定してみましょう。
基本周波数の推定には昔から様々な手法が議論されており、その正確な推定は難しいとされていますが、今回は厳密さは求めず、周波数スペクトルの概形を見て基本周波数を判断することとします。

今回は筆者らの手元にあるエレキベースの3弦3フレット目を押さえたときの”ド(C)” の音を収録し試してみます。

この周波数スペクトルを表示してみると

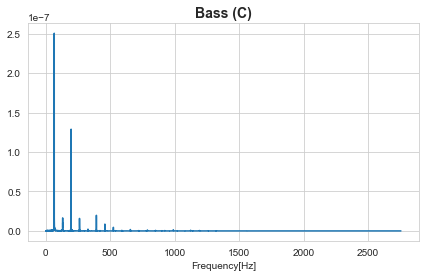
基本周波数とは『その信号に含まれる周波数成分で最も周波数の低いもの』でしたが、今回の音では0~100Hz付近に基本周波数が存在しそうですね。
0~100Hzの範囲で拡大した図がこちらです。

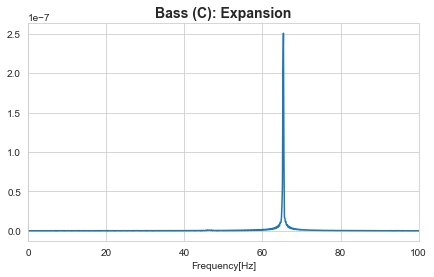
一般にエレキベースの3弦3フレットを押さえた時の音の音階は “ド: C2” と定義され、その周波数は約65Hzとされますが、今回収録した音に確認される基本周波数もこれとほとんど一致することが確認できました。

おわりに

今回はHmcommブログ記事第一弾として基本周波数を出来るだけ易しく説明させていただきました。
Hmcommでは今後随時技術ブログ記事を更新していく予定ですので是非チェックしてください！