Nearest Neighborフィルターによるアナウンス音の分離

R&Dセンターの豊田です。今回はNearest Neighbor filter(NNF)を用いて、スーパーマーケットの閉店を模擬したアナウンスを背景音の蛍の光から分離します。

概要

閉店間際の夜のスーパーマーケットで買い物をしている時に、蛍の光とともに閉店を告げるアナウンスを聞いたことがある方は多いと思います。今回はフリー素材を組み合わせて、閉店時に流れるあの放送を模擬した音を作成し、作成した音からアナウンス部分を背景音の音楽から分離する実験を行います。

準備

今回は以下のサイト様で配布されいるフリー素材を使用させて頂きました。

蛍の光

ポケットサウンド様(https://pocket-se.info/)より、蛍の光のピアノ音を使用させて頂きました。

【BGM】蛍の光（ピアノ）(https://pocket-se.info/archives/1628/)

アナウンス音

横手チサ Chisa Yokote Official Site様 (https://yokotechisa.hateblo.jp/)から、「本日は、ご来店いただき、誠にありがとうございます。」、「 当店は間もなく閉店のお時間でございます。」、「またのご来店を、心から、お待ちしております。」の3つの音声を使用させて頂きました。

会場・店頭アナウンスに使えるフリーのボイス素材 ー ナレーター提供のボイス素材(https://yokotechisa.hateblo.jp/entry/material_announce01)

作成した音

蛍の光とアナウンス音を合成し、スーパーマーケット閉店時の店内放送を模擬した音を作成しました。半額シールが貼られたお惣菜が目に浮かびます。

実験結果

以下の音がNNFを用いて抽出したアナウンス部分です。

歪みがあり、一部蛍の光が混じってしまっていますが概ね分離できています。以下ではこの抽出したアナウンスの抽出をするための実験手順について説明します。

実験手順

今回の実験で使用するNNFは音楽からボーカル部分を抽出するためによく使われる手法の1つです。NNFでは、音楽部分（今回の例では蛍の光）は時間的な繰り返し構造を持ち、ボーカル部分（今回の例ではアナウンス）は時間的な繰り返し構造を持たないという仮定の下、それぞれを抽出するマスク（フィルター）を作成します。

作成した音を短時間フーリエ変換して得られるスペクトログラムは以下の図で与えられます。周波数方向の明るい縦線がアナウンス部分であり、黄色で印をつけています。また、ピンク色の枠で囲われた、5000Hz未満の周波数領域に時間方向に走る横線が蛍の光のピアノ音です。

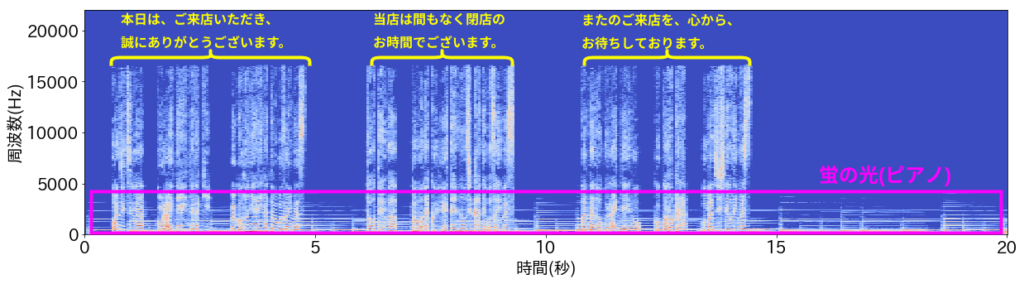
上のスペクトログラムを見ると、蛍の光（ピンク）は、周波数帯5000Hz以下の周波数帯に時間方向に伸びる分布を持ち、時間方向に繰り返し的である一方、アナウンス（黄色）はそれとは逆に、時間方向に局在し、広い周波数分布を持ち、音楽部分と比べると時間方向に非繰り返し的と言えます。NNFはこのような両者の分布の違いを利用し、スペクトログラムから蛍の光を抽出するためのフィルターを作成します。前置きが長くなりましたが、早速実験してみましょう。以下は実験で使用したコードです。

import librosa

# stftを行うためのパラメーター
n_fft = 4096
hop_length = int(n_fft/2)
win_length = n_fft

# wavを読み込み。ここではsourceディレクトリから、
# 蛍の光とアナウンス音を合成した音、cut_closing_supermarket.wavを読みこむと仮定している。
wav, sr = librosa.load('source/cut_closing_supermarket.wav', sr=None)

# stft計算
stft = librosa.stft(wav, n_fft=n_fft, hop_length=hop_length, win_length=win_length)
sp = abs(stft)

# Nearest Neighbor Filterを使い、蛍の光（繰り返し部分）を抽出
S_filter = librosa.decompose.nn_filter(sp, aggregate=np.median, metric='cosine', width=int(librosa.time_to_frames(0.1, sr=sr)))
S_filter = np.minimum(sp, S_filter)

# ソフトマスクによりアナウンス部分を抽出するマスクを作成
margin_v = 40
power = 2
mask_v = librosa.util.softmask(sp-S_filter, margin_v*S_filter, power=power)

# 作成したマスクを元のstftに適用し、アナウンス部分を抽出
S_foreground = mask_v*stft

# 逆stftを行い、音声に戻す
wav_foreground = librosa.istft(S_foreground, hop_length=hop_length, win_length=win_length)

コード実行後、抽出されたアナウンス音wav_foregroundが上の実験結果で示した抽出されたアナウンス音です。以下では、NNFの原理についてもう少し詳しく見ていきましょう。

Nearest Neighbor filter(NNF)の原理

NNFは音楽からボーカル部分を抽出するための技術として開発されました。その原理を文献[1]を参考に解説します。NNFでは、音楽が「楽器が奏でる繰り返し的構造」と「ボーカルの非繰り返し的構造」の二種類によって構成されていると考えます。NNFでは楽器が奏でる繰り返し構造をスペクトログラムから抽出するマスク（フィルター）を作成します。従来の手法では楽器音の周期性を仮定する必要がありましたが、この手法ではスペクトログラムの自己相似性を利用することによりそのような必要性がなくなりました。

類似行列

スペクトログラム\(V\)を\(n\times m\)行列とすると\(n\)、\(m\)はそれぞれ周波数フレームの総数、および時間フレームの総数を表します。スペクトログラムの\(i\)番目の時間フレームの周波数分布ベクトルを

$$\vec{v}_i=\left( \begin{array}{c} V_{1i}\\ V_{2i}\\ \vdots \\ V_{ni} \end{array} \right)$$​

と置きます。以下\(\vec{v}_i\)​は1に規格化されているとします。

$$\vec{v}_i \cdot \vec{v}_i=1$$​

スペクトログラム\(V\)の転置\(V^{T}\)を考え、それらの行列積\(V^{T}V\)を計算して得られる\(m\)次正方行列を\(S\)とおくと、その\((i,j)\)成分\(S_{ij}\)は\(\vec{v}_i\)​​と\(\vec{v}_j\)​​の内積、

$$S_{ij}=\vec{v}_i^T \cdot \vec{v}_j=v_iv_j\cos⁡(\theta_{ij})=\cos⁡(\theta_{ij})\in[0,1]$$

で与えられます。ここで\(\theta_{ij}\)は、\(\vec{v}_i\)と\(\vec{v}_j\)がなす角です。式変形の最後で\(\vec{v}_i\)​、\(\vec{v}_j\)​が規格化されていることを用いています。 \(\vec{v}_i\)と\(\vec{v}_j\)が全く同じ方向を向いているならば上式の値は1になり、直交していれば0になります。スペクトログラムの値は常に正であるため、上式のcosの値がマイナスにならないことに留意します。値が1に近いほど\(\vec{v}_i\)と\(\vec{v}_j\)は「似ている」、0に近いほど「似ていない」ということになります。よって上の式は、二つのベクトルの類似度をcos関数で測る「cos類似度」を計算する式です。コードの17行目metric="cosine"は類似度をcos類似度で測るためのオプションです。行列要素が2つのベクトルの類似性で与えられる行列\(S\)を類似行列と呼びます。 その行列要素計算に使用される時間フレーム\(i\)と\(j\)は同じスペクトログラムから選ばれており、類似行列はスペクトログラム自分自身のある時間フレーム間の相似性、自己相似性を表すと言えます。NNFでは類似行列によって音楽に繰り返し出現するパターンを抽出し、繰り返し性があまりないボーカルと区別します。類似行列の優れた点は、楽器音の周期性を仮定する必要性が無い点です。

繰り返し要素

類似行列\(S\)を用いて音楽中に現れる繰り返し要素（楽器音）を探します。スペクトログラムのある時間フレーム\(j\)に最も類似している\(k\)個の他の時間フレームの集合を\(J_j\)と書き、時間フレーム\(j\)の繰り返し要素と呼びます。時間フレーム\(j\)とある別の時間フレーム\(j^\prime\)のcos類似度がある閾値\(t \in [0,1]\)を超えている場合に「類似している」と判定し、\(j\)の繰り返し要素として抽出します。隣り合う時間フレームは似通ってしまうので、注目している時間フレーム\(j\)から\(d\)フレーム以上離れている時間フレームから類似時間フレームを探します。

繰り返しモデル（繰り返しスペクトログラム)

繰り返し要素\(J_j\)を用いて繰り返しモデル（繰り返しスペクトログラム\(W\))を構成します。\(J_j\)を構成する\(k\)個のベクトルのメディアン（中央値）を計算し、\(W\)の\(j\)番目の時間フレームの周波数分布ベクトルを構成します。コード17行目のaggregate=np.medianは\(k\)個のベクトルの平均操作をメディアンで行うことを意味します。繰り返しスペクトログラムの構成方法について参考文献[1]から引用した図を使ってまとめると以下になります。

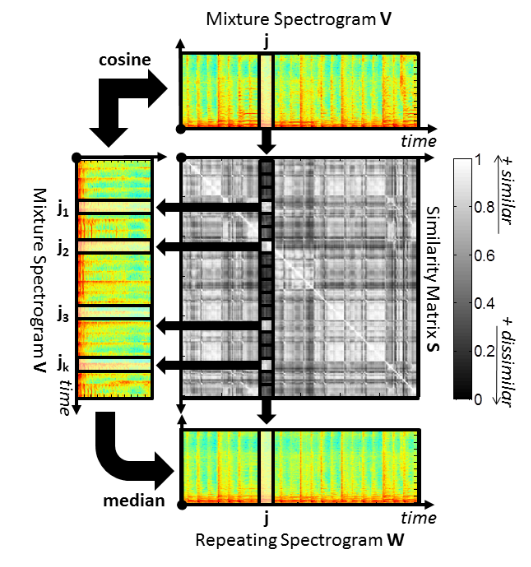
繰り返しスペクトログラム\(W\)に期待される性質として、繰り返し部分（音楽部分）の時間フレームにおいては「明るく」、非繰り返し部分（ボーカル部分）は「暗く」なることです。非繰り返し部分は他の時間フレームとの類似度を計算した時に閾値を超えず、繰り返し要素として抽出されないことです。よって\(W\)中において、ボーカルが聞こえる時間帯の部分は「暗く」なり、音楽部分のみを抽出するマスクの構成ができるようになります。

時間周波数マスク

前節で求めた繰り返しモデル\(W\)から精製繰り返しモデル\(W^\prime\)を以下によって作成します。
NNFでは入力スペクトログラム\(V\)を繰り返し部分（楽器音, \(W\)）と非繰り返し部分(ボーカル, \(V-W\))の線型結合で書けると仮定しています。スペクトログラムの各時間周波数フレームの値は必ず正であるので、\(V_{ij} \geq W_{ij}\)を満たさねばなりません。よって\(W\)の代わりに

$$W^\prime_{ij} ={\rm min}(W_{ij}, V_{ij})$$

を使い、上の条件が保証されるようにします。コードの18行目は上の式の実装になり、S_filterはフィルターされたデータ(繰り返し部分、即ち蛍の光)になります。しかし、上手く分離できていなかったので、得られた結果からソフトマスクを構成し、それをフィルター前のスペクトログラムに適用し、アナウンスの抽出を試みています(コード21行目から下の部分)。

ソフトマスク作成とアナウンス抽出

S_filterを繰り返し部分（蛍の光）とすると、元のスペクトログラムsp(コード14行)からS_filterを引いた結果sp-S_filterが非繰り返し部分（アナウンス）になります。これらの量を使って、ソフトマスクを構成しているのがコード21-23行です。librosa.util.softmaskのインターフェースは以下のようになっています。

librosa.util.softmask(X, X_ref, power=1, split_zeros=False)

実際に計算される量は以下です。

M = X**power / (X**power + X_ref**power)

XとX_refは元スペクトログラムから抽出された成分で、今の場合はXがアナウンス（非繰り返し部分）でsp-S_filterに対応し、X_refが蛍の光(繰り返し部分)で、S_filterに対応します。今回はmargin_vをS_filterを乗じたmargin_v*S_filterをX_refとして使用しています。このマスクを源信号の短時間フーリエ変換stftに乗じて(コード26行)アナウンス部分を取り出し、それを逆短時間フーリエ変換して音声に戻しています(コード29行)。

このように信号処理によって取り出した成分からマスクを構成して目的の信号を取り出す手法はよく使われており、例えば前回の「調波打楽器音分離: 列車走行音からの継ぎ目音分離」(https://fast-d.hmcom.co.jp/blog/hpss/)でも同様のことを行いました。

結論

以上、NNFの原理とソフトマスクを使用したアナウンス抽出方法について述べました。抽出されたアナウンスは歪んでおり、背景の蛍の光が一部混ざっています。抽出の性能を向上するためにはNNFのパラメータやソフトマスクの構成方法をさらに工夫する必要がありそうです。

参考文献